What is a Positive Function?
A positive function has function values greater than zero (i.e., f(x) > 0). The domain (inputs) of the function can be negative, but the outputs (y-values) must be greater than zero. In other words, a positive function has values that are positive for all arguments of its domain.
A non-negative function is similar, except that it includes zero in its range.
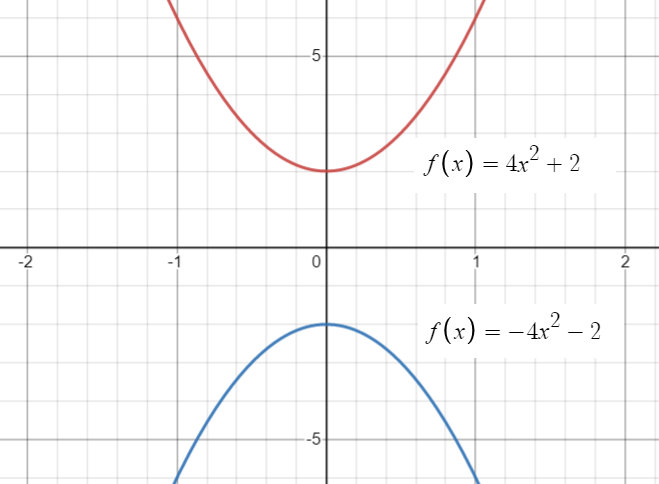
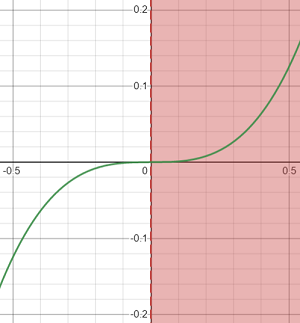
Graphically, if a function’s output values are all above the x-axis, then the function is positive. Conversely, if the output values are all below the x-axis, then the function is negative. A function can also be positive for certain function intervals. For example, the function f(x) = x3 is positive on the open interval (0, ∞) but negative on the interval (-∞, 0).
A caution: a positive function isn’t necessarily an increasing function (although it can be). The function f(x) = 4x2 + 2, shown on the above graph, is completely above the x-axis, which means it is a positive function. However, notice that it is only increasing for function values on the right-hand side of the vertical axis; the function is decreasing for values to the left of the y-axis. In other words, positive functions can have derivatives that are negative or positive.
A couple of interesting properties:
- A positive function f(x) is log-convex if log f(x) is convex [1].
- A linear combination of positive functions is a positive function.
What is a Negative Function?
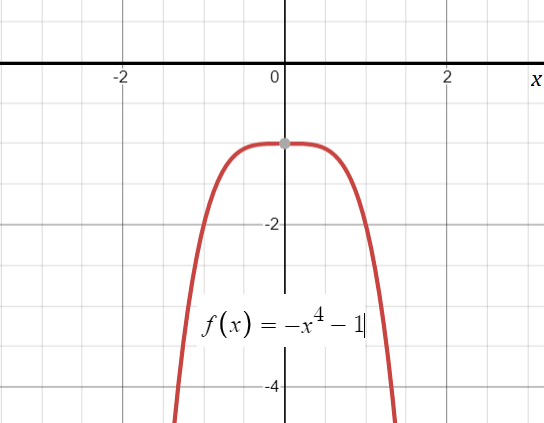
A negative function has values that are all negative (i.e., f(x) < 0). The domain (inputs) of the function can be positive, but every output (y-value) must be less than zero. In other words, a negative function has values that are negative for all arguments of its domain. Graphically, all output (y) values are below the horizontal axis.
Positive Function and Integrals
The definite integral of a positive function represents area under the graph of the function from a to b.
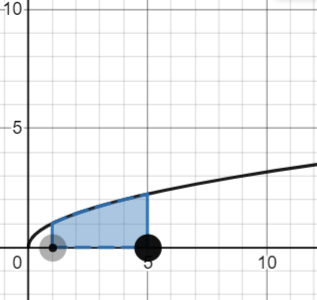
A positive function is integrable if it is a measurable function and if the integral is less than infinity [2].
References
Image created with Desmos.com.
[1] Ni, L. Additional Problems-Set 5. Retrieved March 6, 2021 from: https://mathweb.ucsd.edu/~lni/math220/Pre-pr5.pdf
[2] Hunter, J. Chapter 4: Integration. Retrieved March 6, 2022 from: https://www.math.ucdavis.edu/~hunter/measure_theory/measure_notes_ch4.pdf