A bilinear function (or bilinear form) is a function that’s bilinear for all arguments, which can be scalar or vector (Vinberg, 2003; Haddon, 2000). In other words, it is a linear function of x for every fixed y-value and a linear function of y for every x-value (Shilov & Silverman, 1963).
Bilinear Function Formula and Examples
The function
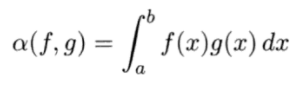
is bilinear for every argument on the space ℂ[a, b], where:
- ℂ = the complex plane,
- [a, b] = closed interval from a to b.
A bilinear form can also be defined in terms of matrices. Every bilinear function on ℝ (the reals) has the form
(x, y) = xtAy
for some n x n matrix A.
A couple of specific bilinear function examples (Karageorgis, 2020):
- An inner product on real-numbered vector space V; This bilinear form is positive definite and symmetric (its variables are unchanged under any permutation; In other words, if you switch out two of the variables, you end up with the same function),
- The dot product on ℝ is a bilinear function.
Related Functions
A symmetric bilinear function is where f(u, v) = f(v, u) for all u and v. Multilinear functions are a generalization of bilinear functions; generally speaking, differential forms are alternating multilinear functions (Harvard, 2017).
References
Haddon, J. 2000. Shape Representation and Bilinear Problems in Computer Vision. University of California, Berkeley.
Harvard University. (2017). Math 23b Problem Session 2 Solutions. Retrieved November 13, 2020 from: https://canvas.harvard.edu/files/3585874/download?download_frd=1&verifier=PeG9X5xVgZSQAsPJKN8X5xT8i5Gv3snwr3Rvbf9h
Karageorgis, P. (2020). Chapter 3. Bilinear forms; Lecture notes for MA1212. Retrieved November 13, 2020 from: https://www.maths.tcd.ie/~pete/ma1212/chapter3.pdf
Laetsch, T. (2012). Bilinear and Quadratic Exercises, p. 1.
Shilov, G. & Silverman, R. (1963). An Introduction to the Theory of Linear Spaces. Prentice-Hall.
Vinberg, E. (2003). A Course in Algebra. American Mathematical Society.