The H function (sometimes called Fox’s H function) is a very generally defined special function, due to Charles Fox (1928).
It can be thought of as an extreme generalization of the generalized hypergeometric functions and is even more general than the Meijer G-functions. The Fox H-functions is also related to both the Mellin-Barnes integrals and Mellin transforms in a more general way than the Meijer-G functions (Choi & Agarwal, 2013).
The formal definition (Khan & Pandey, 2017), represented via a Mellin-Barnes type of contour integral is:
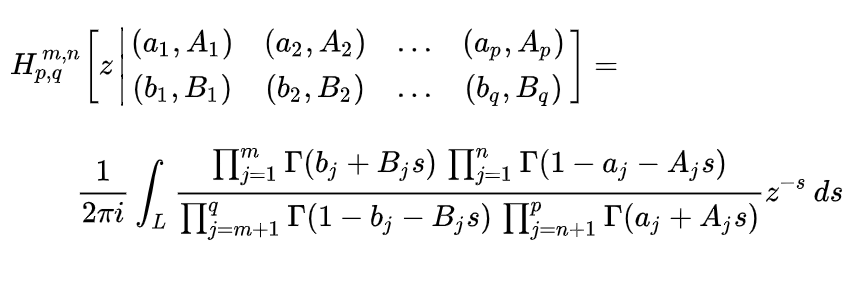
Where 0 ≤ m & le; q, 0 ≤ n ≤ p, αj, Βj > 0 and αj, bj are complex numbers, so that poles Γ(bj – Βjs) for j = 1, 2, … m coincide with poles Γ (1 – αj + αjs) for j = 1, 2, … n.
Use of Fox’s H Function
Fox’s H function has some relatively obscure and highly specialized applications, including fractional diffusion, where several phenomena can be elegantly treated with H functions (Mainardi, 2005). Mellin transforms and stochastic modeling of wireless communications in a fading environment (Mukasa, 2017).
In calculus, it’s occasionally seen in fractional calculus, and is sometimes substituted for the Meijer G function as a better fit for certain pole structures in contours. It can also be useful when dealing with infinite series with certain coefficients, like gamma functions of linear expressions in the index n. Garg and Mittal (2003) obtained a unified integral involving Fox H-function.
A generalized Fox H-function is given by Innayat Hussain AA (1987).
Other H Functions
Fox’s H function shouldn’t be confused with an array of “H functions” in computing, including the fast-growing function developed by Chris Bird, the first few values of which can be found here. In R, there is also a (no relation) H function which “calculates the alpha, beta, and gamma ‘standard diversity indices'” (Charney, 2020_.
References
Al-Musallam, F. A. and Tuan, V. K. “H-Function with Complex Parameters I: Existence.” Int. J. Math. Math. Sci. 25, 571-586, 2001a.
Bird, Chris. Beyond Bird’s Nested Arrays III.
Buschman, R. G. “H-Functions of Two Variables, I.” Indian J. Math. 20, 139-153, 1978.
Fox, C. “The G and H-Functions as Symmetrical Fourier Kernels.” Trans. Amer. Math. Soc. 98, 395-429, 1961.
Charney, N. ‘Standard Diversity Indices’ For Alpha, Beta, And Gamma Diversities. Retrieved August 30, 2020 from: https://www.rdocumentation.org/packages/vegetarian/versions/1.2/topics/H
Fox, C. (1928). The asymptotic expansion of generalized hypergeometric functions. Proc. Lond. Math. Soc. 27, 389-400.
Garg, M, Mittal, S: On a new unified integral. Proc. Indian Acad. Sci. Math. Sci. 114(2), 99-101 (2003)
Innayat-Hussain, AA (1987), “New properties of hypergeometric series derivable from Feynman integrals. I: Transformation and reduction formulae”, J. Phys. A: Math. Gen., 20: 4109–4117, doi:10.1088/0305-4470/20/13/019
Khan, A. & Pandey, N. Integrals Involving H-function of Several Complex Variables. International Journal of Scientific and Research Publications, Volume 7, Issue 2, February 2017 95
Mainardi, F. Fox H functions in fractional diffusion. Journal of Computational and Applied Mathematics.Volume 178, Issues 1–2, 1 June 2005, Pages 321-331
Mathai, A. M. and Saxena, R. K. The H-Function with Applications in Statistics and Other Disciplines.0470263806 New Delhi, India: Wiley, 1978.
Mukasa, C. Stochastic Modeling of Wireless Communications in a Fading Environment via Fox’s H-Function. Retrieved August 30, 2020 from: http://fau.digital.flvc.org/islandora/object/fau%3A39777/datastream/OBJ/view/Stochastic_Modeling_of_Wireless_Communications_in_a_Fading_Environment_via_Fox_s_H-Function.pdf