Chi Squared Table
The chi squared table below is used in hypothesis testing. It helps you to decide whether to accept or reject the null hypothesis. The following chi squared table has the most common values for chi squared. You can find exact figures by using Excel (how to calculate a chi square p value Excel), SPSS (How to perform a chi square in SPSS) or other technology. However, in the vast majority of cases, the chi squared table will give you the value you need.
Watch the video showing how to read critical values on chi squared table. The video includes examples of problems with chi square random variables.
Chi Squared Table
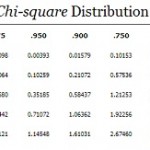
Right tail areas for the Chi-squared Distribution
| df\area | .995 | .990 | .975 | .950 | .900 | .750 | .500 | .250 | .100 | .050 | .025 | .010 | .005 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.00004 | 0.00016 | 0.00098 | 0.00393 | 0.01579 | 0.10153 | 0.45494 | 1.32330 | 2.70554 | 3.84146 | 5.02389 | 6.63490 | 7.87944 |
| 2 | 0.01003 | 0.02010 | 0.05064 | 0.10259 | 0.21072 | 0.57536 | 1.38629 | 2.77259 | 4.60517 | 5.99146 | 7.37776 | 9.21034 | 10.59663 |
| 3 | 0.07172 | 0.11483 | 0.21580 | 0.35185 | 0.58437 | 1.21253 | 2.36597 | 4.10834 | 6.25139 | 7.81473 | 9.34840 | 11.34487 | 12.83816 |
| 4 | 0.20699 | 0.29711 | 0.48442 | 0.71072 | 1.06362 | 1.92256 | 3.35669 | 5.38527 | 7.77944 | 9.48773 | 11.14329 | 13.27670 | 14.86026 |
| 5 | 0.41174 | 0.55430 | 0.83121 | 1.14548 | 1.61031 | 2.67460 | 4.35146 | 6.62568 | 9.23636 | 11.07050 | 12.83250 | 15.08627 | 16.74960 |
| 6 | 0.67573 | 0.87209 | 1.23734 | 1.63538 | 2.20413 | 3.45460 | 5.34812 | 7.84080 | 10.64464 | 12.59159 | 14.44938 | 16.81189 | 18.54758 |
| 7 | 0.98926 | 1.23904 | 1.68987 | 2.16735 | 2.83311 | 4.25485 | 6.34581 | 9.03715 | 12.01704 | 14.06714 | 16.01276 | 18.47531 | 20.27774 |
| 8 | 1.34441 | 1.64650 | 2.17973 | 2.73264 | 3.48954 | 5.07064 | 7.34412 | 10.21885 | 13.36157 | 15.50731 | 17.53455 | 20.09024 | 21.95495 |
| 9 | 1.73493 | 2.08790 | 2.70039 | 3.32511 | 4.16816 | 5.89883 | 8.34283 | 11.38875 | 14.68366 | 16.91898 | 19.02277 | 21.66599 | 23.58935 |
| 10 | 2.15586 | 2.55821 | 3.24697 | 3.94030 | 4.86518 | 6.73720 | 9.34182 | 12.54886 | 15.98718 | 18.30704 | 20.48318 | 23.20925 | 25.18818 |
| 11 | 2.60322 | 3.05348 | 3.81575 | 4.57481 | 5.57778 | 7.58414 | 10.34100 | 13.70069 | 17.27501 | 19.67514 | 21.92005 | 24.72497 | 26.75685 |
| 12 | 3.07382 | 3.57057 | 4.40379 | 5.22603 | 6.30380 | 8.43842 | 11.34032 | 14.84540 | 18.54935 | 21.02607 | 23.33666 | 26.21697 | 28.29952 |
| 13 | 3.56503 | 4.10692 | 5.00875 | 5.89186 | 7.04150 | 9.29907 | 12.33976 | 15.98391 | 19.81193 | 22.36203 | 24.73560 | 27.68825 | 29.81947 |
| 14 | 4.07467 | 4.66043 | 5.62873 | 6.57063 | 7.78953 | 10.16531 | 13.33927 | 17.11693 | 21.06414 | 23.68479 | 26.11895 | 29.14124 | 31.31935 |
| 15 | 4.60092 | 5.22935 | 6.26214 | 7.26094 | 8.54676 | 11.03654 | 14.33886 | 18.24509 | 22.30713 | 24.99579 | 27.48839 | 30.57791 | 32.80132 |
| 16 | 5.14221 | 5.81221 | 6.90766 | 7.96165 | 9.31224 | 11.91222 | 15.33850 | 19.36886 | 23.54183 | 26.29623 | 28.84535 | 31.99993 | 34.26719 |
| 17 | 5.69722 | 6.40776 | 7.56419 | 8.67176 | 10.08519 | 12.79193 | 16.33818 | 20.48868 | 24.76904 | 27.58711 | 30.19101 | 33.40866 | 35.71847 |
| 18 | 6.26480 | 7.01491 | 8.23075 | 9.39046 | 10.86494 | 13.67529 | 17.33790 | 21.60489 | 25.98942 | 28.86930 | 31.52638 | 34.80531 | 37.15645 |
| 19 | 6.84397 | 7.63273 | 8.90652 | 10.11701 | 11.65091 | 14.56200 | 18.33765 | 22.71781 | 27.20357 | 30.14353 | 32.85233 | 36.19087 | 38.58226 |
| 20 | 7.43384 | 8.26040 | 9.59078 | 10.85081 | 12.44261 | 15.45177 | 19.33743 | 23.82769 | 28.41198 | 31.41043 | 34.16961 | 37.56623 | 39.99685 |
| 21 | 8.03365 | 8.89720 | 10.28290 | 11.59131 | 13.23960 | 16.34438 | 20.33723 | 24.93478 | 29.61509 | 32.67057 | 35.47888 | 38.93217 | 41.40106 |
| 22 | 8.64272 | 9.54249 | 10.98232 | 12.33801 | 14.04149 | 17.23962 | 21.33704 | 26.03927 | 30.81328 | 33.92444 | 36.78071 | 40.28936 | 42.79565 |
| 23 | 9.26042 | 10.19572 | 11.68855 | 13.09051 | 14.84796 | 18.13730 | 22.33688 | 27.14134 | 32.00690 | 35.17246 | 38.07563 | 41.63840 | 44.18128 |
| 24 | 9.88623 | 10.85636 | 12.40115 | 13.84843 | 15.65868 | 19.03725 | 23.33673 | 28.24115 | 33.19624 | 36.41503 | 39.36408 | 42.97982 | 45.55851 |
| 25 | 10.51965 | 11.52398 | 13.11972 | 14.61141 | 16.47341 | 19.93934 | 24.33659 | 29.33885 | 34.38159 | 37.65248 | 40.64647 | 44.31410 | 46.92789 |
| 26 | 11.16024 | 12.19815 | 13.84390 | 15.37916 | 17.29188 | 20.84343 | 25.33646 | 30.43457 | 35.56317 | 38.88514 | 41.92317 | 45.64168 | 48.28988 |
| 27 | 11.80759 | 12.87850 | 14.57338 | 16.15140 | 18.11390 | 21.74940 | 26.33634 | 31.52841 | 36.74122 | 40.11327 | 43.19451 | 46.96294 | 49.64492 |
| 28 | 12.46134 | 13.56471 | 15.30786 | 16.92788 | 18.93924 | 22.65716 | 27.33623 | 32.62049 | 37.91592 | 41.33714 | 44.46079 | 48.27824 | 50.99338 |
| 29 | 13.12115 | 14.25645 | 16.04707 | 17.70837 | 19.76774 | 23.56659 | 28.33613 | 33.71091 | 39.08747 | 42.55697 | 45.72229 | 49.58788 | 52.33562 |
| 30 | 13.78672 | 14.95346 | 16.79077 | 18.49266 | 20.59923 | 24.47761 | 29.33603 | 34.79974 | 40.25602 | 43.77297 | 46.97924 | 50.89218 | 53.67196 |
Sample problem using the chi squared table
Sample question: You work for a seed manufacturer. You want to find out if there is a link between hybrid plants and how many deviations (i.e. unwanted plants) that crop up. There are two corn types: blue and yellow. The probability that deviations would happen by chance is about 5%. Find the critical chi-square value using the chi squared table.
Step 1: Subtract 1 from the number of categories to get the degrees of freedom. Categories are blue corn and yellow corn, so df = 2-1 = 1.
Step 2: Look up your degrees of freedom and probability in the chi squared table. The probability is given to you in the question (5% or 0.05).
One degree of freedom and 5 percent probability is 3.84 in the chi squared table. This is your critical chi-square value.
Tip: A small value from the chi squared table means that there isn’t much of a relationship between the two variables. A larger value indicates a greater relationship between your two variables.
References
Beyer, W. (2017). Handbook of Tables for Probability and Statistics 2nd Edition. CRC Press.