Multilinear Function: Definition & Examples

Types of Functions >

A multilinear function (also called a multilinear form) is linear in each variable separately (i.e. linear in all its arguments). In other words, it is a linear function of each variable k when all the other variables are assigned fixed values. They are polynomials of order n but with a maximum order of one for each variable [1].

The end result is that a quantity varies proportionally with several variables, k. Bilinear functions (k = 2) and trilinear functions (k = 3) are special cases.

Formal Definition of a Multilinear Function

Let’s say we had the following function:
f: W₁ * … * W_k → V
Where W₁, …, W_k V are vector spaces over a field 𝔽.
It is a multilinear function if:


For any w₁ ∈ W₁, w₂ ∈ W₂… w_n ∈ W_N [2].
In other words, it is multilinear if it is homogenously linear in each of its arguments, k, separately.

We can also define a multilinear function f with matrices and the Kronecker product ⊗ [3]:

f(x) = α^T m(x),
where α = [α₁ … α_2ⁿ]^T ∈ ℝ²ⁿ is a coefficient row vector and


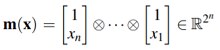
is a column vector of monomial.

Multilinear Functions of Vectors

A function of one variable is linear if both of the following statements are true:

• f (x + y) = f(x) + f(y)
• f (cx) = cf (c).

We can build on this statement to define multilinear functions of several vectors. A function of several vectors u, v, … is multilinear if [4]:

• f (u₁ + u₂, v,…) = f (u₁, v,…) + (u₂, v,…),
• f (cu, v, …) = cf(u, v,…)
• f (u, v₁ + v₂,…) = f (u₁, v₁,…) + (u, v₂, …),
• f (u, cv, …) = cf(u, v,…)

Multilinear functions of several vectors can easily be built using cross products and dot products. For example: u, v, w → u × (v × w).

References

[1] Pangalos, G., Eichler, A., & Lichtenberg, G. (2015). Hybrid
multilinear modeling and applications. In Simulation
and Modeling Methodologies, Technologies and Applications (pp. 71-85). Springer, Cham.
[2] 1 Multilinear and alternating functions. 21-801: Algebraic Methods in Combinatorics Multilinear notes. Retrieved May 3, 2021 from: http://www.borisbukh.org/AlgMethods14/multilinear_notes.pdf
[3] Sridharan, A., Lichtenberg, G., Salvador, A. and Salgado, C.
Approaches to Parameter Identification for Hybrid Multilinear Time Invariant Systems. DOI: 10.5220/0009887502550262 In Proceedings of the 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2020), pages 255-262. ISBN: 978-989-758-444-2
[4] Dotensko, V. Linear Algebra 1: Lecture 3.