The Riemann Xi function (sometimes called just the Xi Function), introduced by Riemann in 1859, is a modification of the Riemann Zeta function. The xi function is defined analytically for all s and has the same zeros as the zeta function (Logan, 2019).
The Riemann Xi function can be defined as
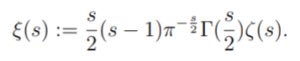
for any s ∈ ℂ (∈ means “is an element of” and ℂ is the complex plane).
Where:
- Γ is the gamma function,
- ζ is the zeta function.
Properties of the Riemann Xi Function
- The above definition of the Riemann Xi function (it can be defined in other ways) has no singularities and so is valid for all values of s.
- There is a symmetric relationship between the xi function’s positive values and negative values. This is often stated as the following relationship: ξ(s) = ξ(1 – s). This fact, combined with the Euler product, shows that the Riemann Xi function can only have zeros between (the real-numbered) 0 and 1 (in other words, the function’s zeros are at the nonreal zeros of the Riemann Zeta function). This important property leads, in part, to the conclusion that the Riemann Hypothesis is true (Logan, 2019).
- The Riemann Xi function is an entire function (Edwards 2001, p. 16).
References
Ahn, S. (2012). On the zeros of component functions of the Riemann Xi approximates. Retrieved November 9, 2020 from: https://www.math.upenn.edu/~jhaglund/thesis/Shirley.pdf
Edwards, H. M. (2001). The Function xi(s). §1.8 in Riemann’s Zeta Function. New York: Dover, pp. 16-18.
Logan, A. (2019). Investigation of the Characteristics of the Zeros of the Riemann Zeta Function in the Critical Strip Using Implicit Function Properties of the Real and Imaginary Components of the Dirichlet Eta function. Retrieved November 9, 2020 from: https://easychair.org/publications/preprint/C1wB
Riemann, B. (1859). Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse (On the number of primes less than a given quantity). Monatsberichte der Berliner Akademie.
Tao, T. (2018). Vaporizing and Freezing the Riemann zeta function. Retrieved November 9, 2020 from: https://terrytao.files.wordpress.com/2018/08/webinar.pdf