Derivatives >
Contents:
Polar Coordinates Definition
Polar coordinates are very similar to the “usual” rectangular coordinates: both systems are two dimensional, they locate a point in space, and both use two points: the rectangular system uses (x, y) and the polar coordinate system uses (r, θ).
Plotting Polar Coordinates
To plot polar coordinates, you need two pieces of information, r and θ:
- θ tells you the ray’s angle from the polar axis (the positive part of the x-axis).
- “r” tells you how to move on the ray. If r > 0, move on the ray. If r < 0, move on the opposite ray.
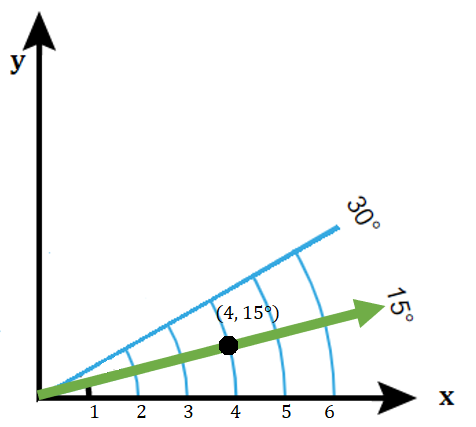
The easiest way to understand how to plot polar coordinates is to plot one first on the familiar x-y axis. Let’s say you wanted to plot point P, located at (4, 15°). Here, r = 3, so that’s going to be equal to x = 3. The angle of the ray from the x-axis is 15 degrees, so the goal is to draw the 15 degree ray, then locate the point:
What about (-4, 15°)? To get a negative “x” value, just move in the opposite direction, just like you’d do with regular coordinates.
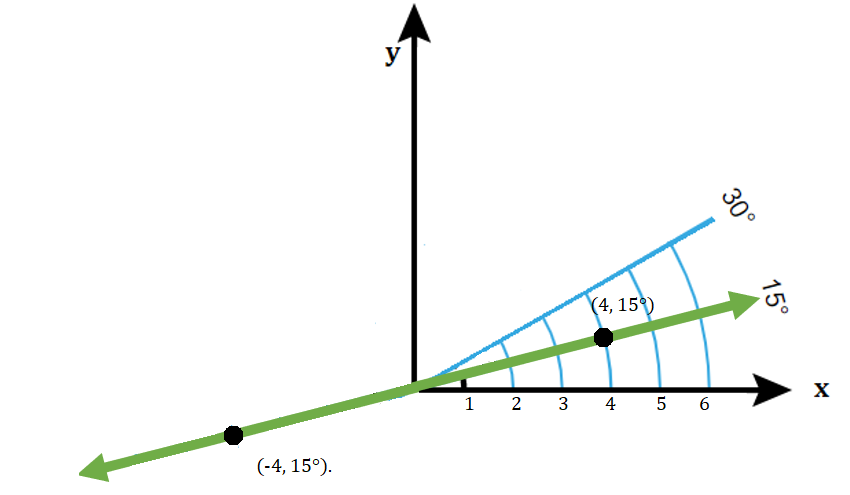
The whole grid looks like this:
In the above example, the negative number in (-4, 15°) meant that you travel in the opposite direction from the 15 degree ray. You could also write the exact same point as (-4, 195°).
Why Use Polar Coordinates?
Polar coordinates make it easier to understand some natural phenomena with circular motion from a central point, like the motion of planets around the sun or atoms around a nucleus.
Cylindrical Coordinates
Cylindrical coordinates are an extension of two-dimensional polar coordinates to three-dimensions.
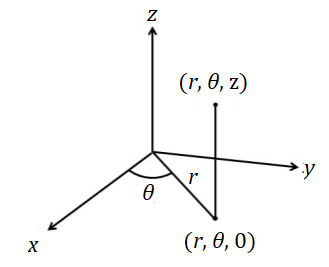
With cylindrical coordinates, the usual x- and y-coordinates of a point in the Cartesian plane are replaced by polar coordinates. A point with P = (x, y, z) has cylindrical coordinates P = (r, θ, z) where (r, θ) are polar coordinates of (x, y).
Use of Cylindrical Coordinates
Primarily used in physics, the cylindrical coordinate system (formally called the circular cylindrical or circular polar coordinate system) eases calculations involving cylinders or cylindrical symmetries (Hassani, 2009). For example:
- Pipe flows with no-slip conditions at the wall drive pipe flow and require the use of cylindrical coordinates (Orlandi, 2012).
- A magnetic field, generated by a current flowing in a long straight wire, is more conveniently expressed in cylindrical form (Rogawski, 2007).
Converting from Rectangular (Cartesian) to Cylindrical Coordinates
To convert, replace the x and y coordinates with the polar coordinates r and θ, using the following relations for x and y:
- r = √(x2 + y2)
- tanθ = y/x
The z-coordinate remains unchanged.
Example question: Convert (√3, 1, 4) from rectangular to cylindrical coordinates.
Solution: Take each point (x, y, z) one at a time and convert (√3, 1, 4) using the above relations, to get:
- r = √(x2 + y2) = √(3 + 1)
- θ = tan-1(y/x) = tan-1(1/√3) = π/6
- z = 4.
Putting those together, we get (2, π/6, 4).
Converting from Cylindrical to Rectangular Coordinates
Use the relations:
- x = r cosθ
- y = r sinθ.
The z-coordinate remains unchanged.
Example question: Convert the cylindrical coordinates (3, π/3, -4) to rectangular coordinates.
Solution:
- x = r cosθ = 3 cos (π/3) = 3(½) = 3/2
- y = r sinθ = 3 sin (π/3) = 3 (√3/2) = (3√3)/2
The z-coordinate remains unchanged, giving:
(3/2, (3√3)/2, -4).
Polar Function Definition
A polar function relates a radius vector (a distance, r) and an angle vector (θ). These functions are based in the polar coordinate system.

- Anywhere objects move in circles (for example: movement of electrons),
- A plan position indicator (a type of radar display) used in air traffic control, ship navigation and meteorology,
- Radiance functions for material brightness can be represented by a polar function on the unit sphere (Robles-Kelly & Hancock, 2004).
Types of Polar Function
A polar function is defined by the polar equation r = f(θ). Many polar functions have been classified in detail, including:
1. Lemniscate Polar Function
A polar function of the form r2 = a2 sin (2θ) and r2 = a2 cos (2θ) are lemniscates (from the Latin lēmniscātus meaning decorated with ribbons).
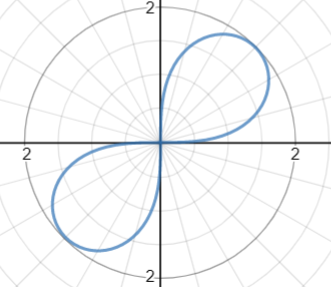
Click here for an interactive version of this graph on Desmos.com.
2. Limaçon & Cardioid
Limaçons (from the Latin limax meaning snail) are formed by the following equations:
- r = a + b sin θ,
- r = a – b sin θ,
- r = a + b cos θ,
- r = a – b cos θ.
Cosine and sine are shifted 45 degrees from each other. For example:
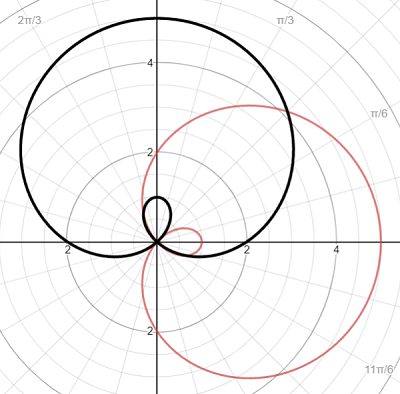
Click here for an interactive version of the graph.
A cardioid (a heart shaped curve) is a special case of the Limaçon, graphed when a = b.
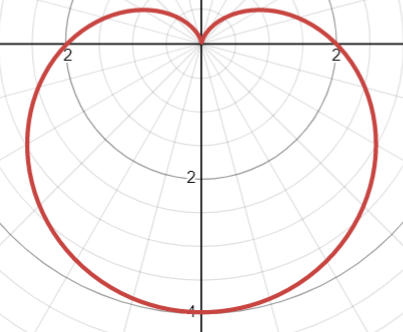
3. Rose Polar Function
A polar function with the form r = a sin nθ or r = a cos nθ graph roses. The two functions look almost identical, except they are shifted:
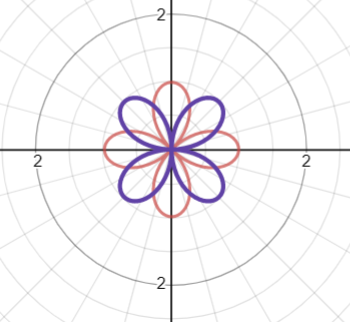
For an interactive graph (where you can change the values for r and θ) click here to go to Desmos.
4. The Archimedean Spiral
The Archimedean spiral is defined by r = aθ.
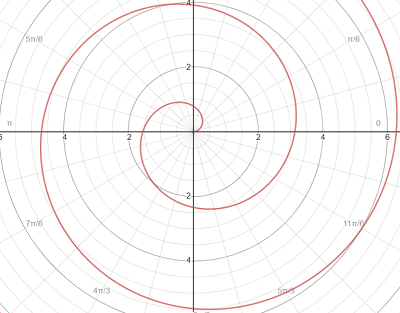
For an interactive graph, go to: Desmos.com.
Polar Derivatives
The polar derivative generalizes the usual derivative to polar coordinates. In other words, the derivative rules you used in elementary calculus only work in the Cartesian plane. In order to find the derivative of a polar function, you have to use a different formula.
As polar coordinates are based on angles, it should be no surprise that derivatives involve a little trigonometry. A polar coordinate can be expressed in terms of:
- The distance from the origin (r) and
- An angle (θ).
The first derivative of a polar curve uses these coordinates in the formula:
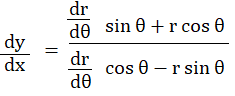
Polar Derivative: Example Problem
There are a couple of ways to find a polar derivative. The first is to use the above formula. However, instead of memorizing yet another formula, you could convert your coordinates and use the product rule instead; The following example shows how this method works to get the same result.
Example Question: Find the polar derivative of r = 2 sin(θ) at π/2.
Step 1: Convert the polar coordinates (r, θ) to Cartesian coordinates. The conversion formulas are:
- x = r cos(θ)
- y = r sin(θ)
We’re given r = 2 sin(θ) in the question, so:
- x = (2 sinθ) cos(θ)
- y = (2 sinθ) sin(θ)
Step 2: Find the derivative of y from Step 1. The function y = (2 sinθ) sin(θ) is two functions multiplied together, so for this example, use the product rule: (f * g)′ = f′ * g + f * g′.
Inserting the value for “y” from Step 1 into the product rule formula, we get:
(2 sin θ)(cos θ) + (sin θ)(2 cosθ)
Step 3: Find the derivative of x from Step 1. The function x = (2 sinθ) cos(θ) can be differentiated with the product rule as well, so:
(2 sin θ)(-sin θ) + (cos θ)(2 cosθ)
Step 4: Divide Step 2 (dy) by Step 3 (dx), to get:
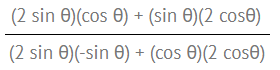
Step 5: Insert your value for θ, which is given in the question as π/2:
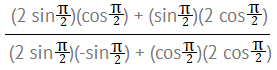
Step 6: Simplify, using a calculator to find values. For example, cosθ = 0.
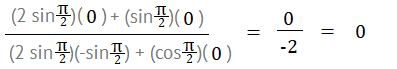
Solution: The derivative is 0.
That’s it!
Polar Derivative and Complex Numbers
The polar derivative can be defined for complex numbers as:
Dα p(z) = np(z) + (α – z) p′(z);
Where α = a complex number and p ∈ Pn (Li, 2011).
There are other slightly different notations. For example, you could write the polar derivative with respect to zeta(ζ):
fζ(z): = nf(z) + (ζ – z) f′(z),
where ζ is a complex number.
If degree f(z) = n, then fζ(z) is a polynomial function with degree n – 1. If ζ = ∞, then f∞ is equal to the ordinary derivative (Barsegian et al., 2006).
Polar Derivative: References
Barsegian, G. et al., (2006). Value Distribution Theory and Related Topics. Advances in Complex Analysis and Its Applications. Book 3. Springer Science & Business Media.
Glahodny, G. Section 13.9: Cylindrical and Spherical Coordinates. Retrieved December 2, 2020 from: https://www2.math.tamu.edu/~glahodny/
Hassani, S. (2009). Mathematical Methods For Students of Physics and Related Fields. Springer.
Li, X. (2011). A Comparison Equality for Rational Functions. Proceedings of the American Mathematical Society. Volume 139, Number 5. Retrieved September 2, 2020 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.353.2854&rep=rep1&type=pdf
Occhiogrosso, M. (2007). Polar Coordinates and Trigonometric Form: Trigonometry. Milliken Publishing Company.
Orlandi, P. (2012). Fluid Flow Phenomena: A Numerical Toolkit (Fluid Mechanics and Its Applications Book 55), Kindle Edition. Springer.
Robles-Kelly, A. & Hancock, E. (2004). Radiance Function Estimation for Object Classification. In Progress in Pattern Recognition, Image Analysis and Applications. 9th Iberoamerican Congress on Pattern Recognition, CIARP. Springer.
Rogawski, J. (2007). Multivariable Calculus: Early Transcendentals. W. H. Freeman.
Shiver, J. Polar Equations and Their Graphs. Retrieved September 4, 2020 from: http://jwilson.coe.uga.edu/EMT668/EMAT6680.2003.fall/Shiver/assignment11/PolarGraphs.htm
Image of coordinate grid: Mets501 [CC BY-SA (http://creativecommons.org/licenses/by-sa/3.0/)]