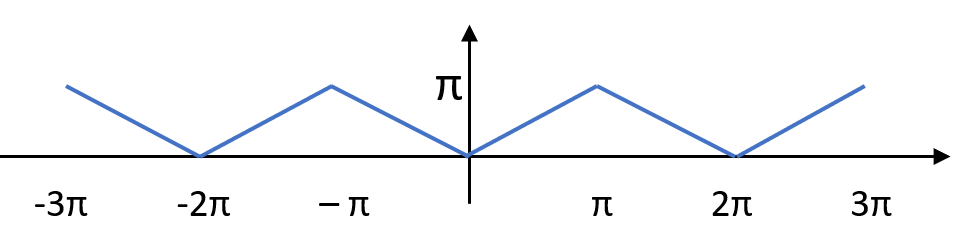
The Triangle Wave Function is a periodic function used in signal processing. It is an even function, which means it is symmetrical around the y-axis.
This function is sometimes also called the continuous sawtooth function, however, the actual “sawtooth” has a slightly different shape:
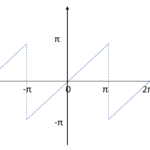
Constructing a Triangle Wave Function
Graphing the triangle wave function is a challenge, because there isn’t a single definition, in terms of a graphable function, for the triangle wave.
One way to define the function is in terms of the floor function (⌊ x ⌋ ):
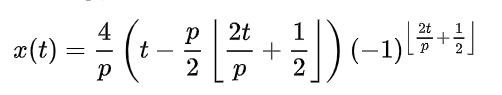
This may be a helpful definition, but with the inclusion of a floor function, it isn’t graphable as-is. An alternate definition is as the absolute value of the sawtooth wave, but that definition also includes the floor function.
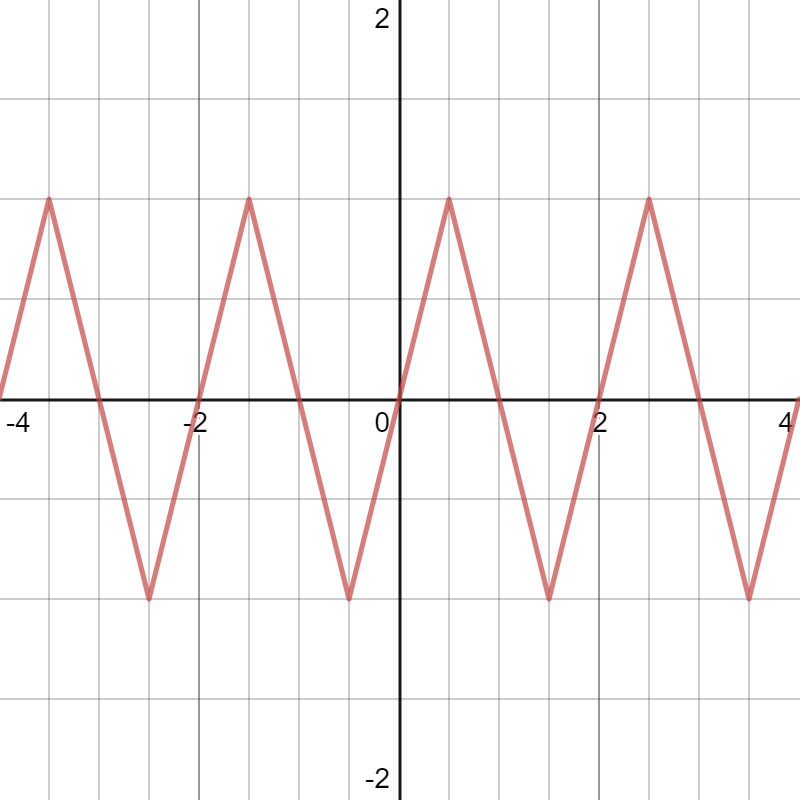
Perhaps the simplest way to approximate the shape is with the sine function and inverse sine function. For example, the following graph uses a combination of sine and inverse sine to create the triangular waves:
Creating a Triangle Wave with Piecewise Functions
One relatively simple way to create a graph of the triangle wave function is to construct a series of piecewise functions. In other words, each individual “tooth” can be built with one or two functions.
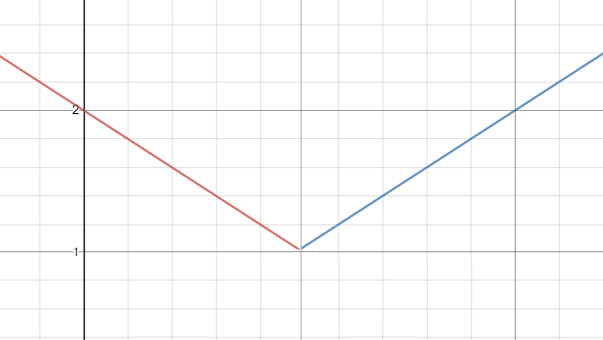
As an example, the following graph of one tooth (actually a sawtooth function) is represented by two different functions: one for the upslope and one for the downslope:
References
Desmos.com
Gustafson, S. Math 257/316 Assignment 5 Solutions. Retrieved December 20, 2019 from: http://www.math.ubc.ca/~gustaf/M316/homework5sol.pdf
Orloff, J. ES.1803 Topic 22 Notes. Retrieved December 20, 2019 from: http://web.mit.edu/jorloff/www/18.03-esg/notes/topic22.pdf
Weisstein, Eric W. From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/TriangleWave.html