Contents:
What is a Deterministic Function?
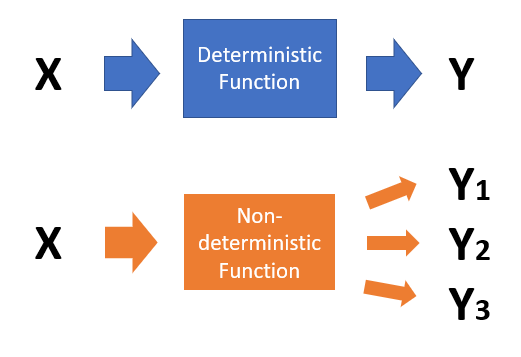
Deterministic means the opposite of randomness, giving the same results every time. So in a sense, all mathematical functions are deterministic, because they give the same results every time; The output of the “usual” function is only determined by its inputs, without any random elements; There are exceptions in stochastic calculus.
The opposite of a deterministic function is a nondeterministic function (sometimes called a random function). Broadly speaking, those terms don’t actually refer to a “function” in the true sense of the word but rather a random process, like predicting weather events, Brownian motion, or other phenomena with elements of randomness. These random processes always have a deterministic part, which might be an average value or expected pattern. In other words, the process isn’t truly random, but is expected to produce outputs within a certain range. The “nondeterminisitc” part is the random element (which is why it’s so hard for weathermen to get forecasts right!).
Deterministic Functions in Stochastic Calculus
In calculus, we usually aren’t concerned with whether functions are deterministic or not, as it’s assumed all functions are deterministic. However, there is a branch of calculus called stochastic calculus, that deals with functions that have random elements.
In stochastic calculus, functions are evaluated to account for random elements. For example, stochastic integrals are generalized ordinary integrals where the integrator is not the usual “dx” but rather a stochastic process with random elements. This allows you to evaluate processes that cannot be evaluated with ordinary calculus methods, like Brownian motion (The Wiener process) [1].
The integrand (the function you want to integrate) can also be nondeterministic. These require completely different definitions for integrals and include the Ito Integral and Stratonovich Integral.
What is a Deterministic Sequence?
A deterministic sequence is one where any term in the sequence can be determined from other terms in the sequence. Theoretically, the future of any deterministic sequence can be determined from its past [2].
These sequences are generated by a rule or set of rules, unlike their opposite, random sequences, which have no underlying order. Deterministic sequences have the advantage of good uniformity coverage, i.e. they have a broad range of values that are taken from the entire set of possible values. However, their terms are not independent of each other and they do not have the adaptive behavior of random (probabilistic) sequences [3].
Deterministic Sequence Applications
A random number generator (or, more accurately, a pseudorandom number generator) uses an algorithm to approximate a random sequence. Theses sequences are not truly random because the underlying generation is determined by an algorithm: they are actually deterministic. For example, a linear congruential generator (LCG) generates a random b-bit integer with the recursion
Xn+1 = (a Xn + c) mod 2b
With initial random seed (starting number) X0. [4]
Deterministic sequences are used in Serial Reaction Time (SRT) tasks to study learning. In a classic SRT task, participants are asked to react to a visual stimulus, like a dot. The dot appears sequentially in predetermined positions on a screen in a repeating pattern: participants are asked to press a corresponding key as accurately and quickly as possible. Probabilistic sequences are also introduced, presenting the participants a mixture of deterministic and random sequences [5].
References
[1] The Azimuth Project. (2015). The Stochastic Integral. Retrieved April 14, 2021 from: https://www.azimuthproject.org/azimuth/show/Stochastic+integral
[2] Furstenberg, H. (2016). Stationary Processes and Prediction Theory. Annals of Mathematics Studies (201 Books) (AM-44), Volume 44. Princeton University Press.
[3] Gratacòs, J. & Galbete, I. (2004). An adaptative deterministic sequence for sampling-based motion planners. Retrieved June 25, 2021 from: https://upcommons.upc.edu/handle/2117/567
[4] Random Number Generators. Retrieved June 25, 2021 from: https://people.orie.cornell.edu/snp32/orie_6125/random-numbers/random-numbers.html
[5] Martini, M. & Furtner, M. (2013). Working Memory and Its Relation to Deterministic Sequence Learning. Retrieved June 25, 2021 from: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0056166