Pentation functions are a family of functions that undergo pentation. Put simply, pentation (sometimes called Hyper-5) is a type of repeated exponentiation, where you raise a number to a power (e.g. x2) and repeat the process. Technically speaking, tetration is where you repeat the exponentiation process, and pentation is where you repeat the tetration process (so it’s sort of “repeated, repeated” exponentiation).
The name “pentation” was coined by Reuben Goodstein (1947) and is a meld of the words penta-(Greek for “five”) and iteration (repetition).
Notation
Pentation is usually represented either by a triple up arrow: ↑↑↑ (Knuth, 1976) or by nx, where “x” is pentated to the nth power.
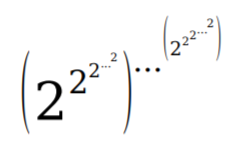
Informally, it is sometimes represented as b^^^p. This may be due to the fact that the caret (^) is readily available on keyboards, while up arrows and subscripts are not.
Example
Note: as pentation is repeated tetration (represented by ↑↑), you may find it useful to read the examples in the tetration function article first.
As a simple example, here’s 2 pentated to 3 (2↑↑↑3):
2↑↑↑3 = 2↑↑2↑↑2 = 2↑↑22 = 2↑↑4 = 2222 = 65,536
If you use larger numbers, there simply isn’t enough room on the page to write the result (which can involve trillions of digits). To give you an idea of the scale, tetration (the “simpler” cousin of pentation and a step above in the food chain) can be used to represent things like the number of atoms in the universe. In practical terms, there really isn’t much use for pentation, which is why you’re unlikely to see it mentioned in most mathematical textbooks.
Series of Hyperoperations
Hyperoperations are a series of operations, starting with addition, where the previous operation is repeated. For example, the simplest operation is addition. Multiplication is next in the series. You can think of multiplication as repeated addition. For example, the multiplication 4 x 4 is the same as the addition 4 + 4 + 4 + 4. Pentation is the fifth in the series.
In order, the hyperoperations are:
- Addition.
- Multiplication.
- Exponentiation. This is really just repeated multiplication. For example, 24 = 2 * 2 * 2 * 2.
- Tetration. Tetration is repeated exponentiation.
- Pentation: repeated tetration.
References
Goodstein, R. L., “Transfinite Ordinals in Recursive Number Theory.” The Journal of Symbolic
Logic, Vol. 12, No. 4 (December 1947), pp. 123-129.
Muller, M.Reihenalgebra: What comes beyond exponentiation? Retrieved December 4, 2019 from: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=D0EAC1E8F842F5B1B1314285CB403DA8?doi=10.1.1.682.4047&rep=rep1&type=pdf
Disjoint Forest. Retrieved December 4, 2019 from: http://web.stanford.edu/class/archive/cs/cs166/cs166.1166/lectures/16/Small16.pdf