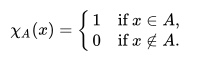Contents:
Step Function: Definition
A step function features constant or “flat” areas punctuated by abrupt jumps, called jump discontinuities. It looks exactly like what the name suggests: it’s a series of one or more steps. More technically, it’s defined as a piecewise function, with a finite number of pieces.
Formal Definition
Formally, a step function is defined as a function over the real numbers that can be written as a finite linear combination of indicator functions of intervals.
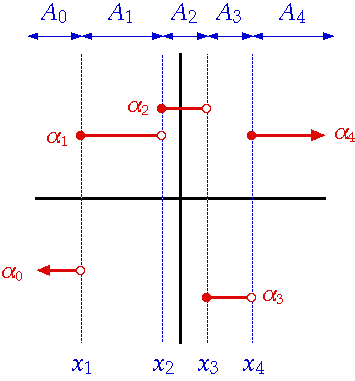
It can also be defined as a function over the real numbers that can be written as:
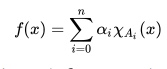
Where:
- n is an integer greater than zero,
- αi are real numbers.
- Ai are intervals,
- ΧA is the indicator function, defined as:

Simple Examples of the Step Function
By the above definition, the constant function f(x) = A is a step function, though there is only one interval. In terms of “steps”, there’s just one; Imagine you’re standing on the first step of a set of stairs. There’s no up or down—just the flat surface you’re standing on.
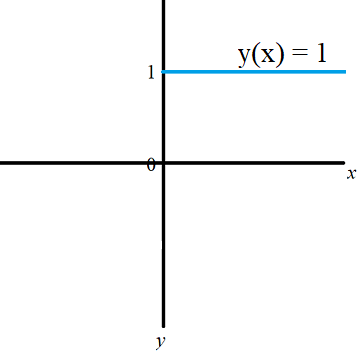
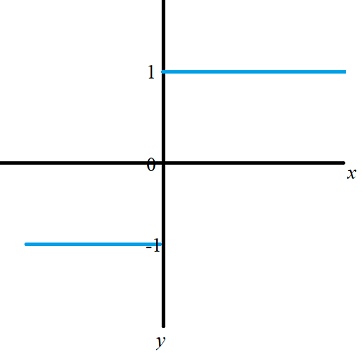
Another very simple step function—with a step in it—is the sign function. This function sends all positive numbers to +1, and all negative numbers to -1, so it has just one jump discontinuity.
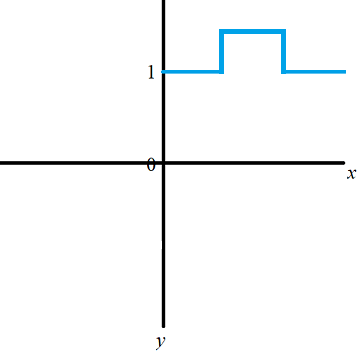
The rectangular function is constant at 0 for most values of x, but sends one interval Ai to a constant a.
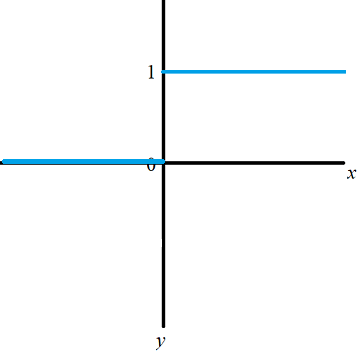
The Heaviside function is very like the sign function in that it has just one discontinuity, at zero, but it sends all positive numbers to 1 and all negative numbers to zero.
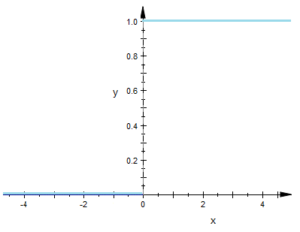
Heaviside Function (Unit Step Function)
The Heaviside step function (named after physicist Oliver Heaviside) is a simple discontinuous piecewise function defined over the interval (-∞, ∞). The function, usually denoted as H(t), equals:
- 0 for all negative values of t,
- 1 for all positive values of t.
Although the unit step function (a standard Heaviside, shown below) can only take on values of 0 or 1, it can be used to model other values. For example:
- -9 μc(t) is a switch that turns on at time c with a value of -9,
- 0.5 μc(t) is a switch that turns on at time c with a value of 0.5.
The graph, which is centered at zero, can be shifted along the x-axis to make a shifted Heaviside function. This is especially useful when modeling waveforms that are turned on or off at some interval other than t = 0.
Heaviside Function Integral and Derivative
In terms of integrals, the Heaviside function is the integral of the Dirac function. The derivative of the Heaviside function is 0 for all x ≠ 0. At x = 0 the derivative is undefined. Although there isn’t a true derivative as such (i.e. one that is a function), the Dirac delta function can be used to approximate it.
Importance of the Heaviside Function
The Heaviside function is widely used in engineering applications and is often used to model physical systems in real time, especially those that change abruptly at certain times. For example, when current is turned on or off. In mathematics, the function is used as a basic building block with Laplace transforms, to shift functions.
References
Chapter 20: The Dirac Delta Function. Retrieved December 6, 2019 from: http://www.nada.kth.se/~annak/diracdelta.pdf
References
Step and Box Functions. Retrieved from https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-iii-fourier-series-and-laplace-transform/step-and-delta-functions-integrals-and-generalized-derivatives/MIT18_03SCF11_s24_1text.pdf on November 25, 2018.
Labossiere, P. ME354 Mechanics of Materials Laboratory. Beam deflections using discontinuity functions. Retrieved OCtober 7, 2019 from: http://courses.washington.edu/me354a/discontinuity_functions.pdf