Faà di Bruno’s Formula: Definition, Example Steps

Derivatives > Faà di Bruno’s Formula

Faà di Bruno’s Formula is a way to find higher order derivatives of composite functions. The technique, named after Faà di Bruno (1825-1888), is a generalization of the chain rule.

How to Use Faà di Bruno’s Formula

The technique uses a basic technique from combinatorics, where a basic combinatoric problem is to find the number of possible configurations of a given type. That’s exactly what you do here, except don’t let the inclusion of combinatorics scare you: finding the first few higher order derivatives (up to the 4th) is relatively easy with a few calculation steps (see below for an example). Calculating higher derivatives beyond the 3rd or 4th isn’t usually practical by hand due to the large number of enumeration of terms required (Klimko, 1972). Three simpler alternatives have been described in the literature; They avoid Faà di Bruno’s formula complications of “substantial” combinatorial techniques (for derivatives beyond the 4th) and diophantine questions, but they aren’t as explicit as the solutions of Faà di Bruno’s method (Huang et al., 2006).

Faà di Bruno’s Formula Example

A few different versions of Faà di Bruno’s formula exist. For example, the formula is a sum over partitions of products in some versions of the chain rule. In the general form for calculus of variations, the outer function has directional variations that are also differentials of the inner function (Clark & Houssineau, 2003).

The following definition (Johnson, 2018) is relatively easy to calculate:
Let’s suppose f and g are functions have nth order derivatives that exist. Then Faà di Bruno’s Formula can be defined as:

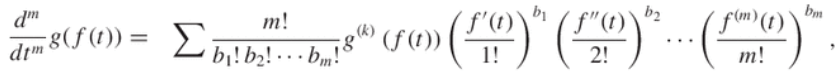
Where the sum is over all different solutions in nonnegative integers b₁…b_m of b₁ + 2b₂ + … + mb_m = m, and k:=b₁ + … b_m.

Note the factorials in the denominator of Faà di Bruno’s formula. This is one reason why higher order derivatives (say, the 100th) become extremely tedious by hand; Henry Flanders, in his American Mathematical Monthly contribution From Ford to Faà, called the method a “practically inefficient” way of finding numerical derivatives. However, 3rd or 4th orders can be calculated manually without too much of a problem.

The basic procedure is:
Step 1: Find all solutions in nonnegative integers of b₁ + 2b₂ + 3b₃ = m.

Let’s say m = 3. The three possible solutions are:

1. Solution A: (0) + 2(0) + 3(1) = 3.
2. Solution B: (1) + 2(1) + 0 = 3.
3. Solution C: 3 + 2(0) + 3(0) = 3.

Step 2: Find k, which is defined as
k:=b₁ + … b_m.
For the above example of m = 3, k would be:

1. Solution A: b₁ (0) + b₂(0) + b₃(1) = 1.
2. Solution B: b₁ (1) + b₂(1) + b₃(0) = 2.
3. Solution C: b₁ (3) + b₂(0) + b₃(0) = 3.

Step 3: Insert the above findings into Faà di Bruno’s Formula (plugging in the values for b₁, b₂, and b₃ from Step 1 and k from Step 2. This will give three different terms (one for each solution A, B, C).


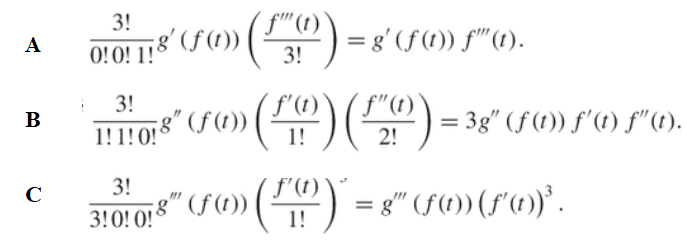
Step 4: Sum up the solutions to give the derivative:

References

Clark, D. & Houssineau, J. Faa di Bruno’s formula for chain differentials. 2003. Retrieved May 22, 2020 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.740.9950&rep=rep1&type=pdf
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, pp. 137-139, 1974.
Flanders, H. From Ford to Faà. The American Mathematical Monthly
Vol. 108, No. 6 (Jun. – Jul., 2001), pp. 559-561
Huang et al. Chain Rules for Higher Derivatives. Springer-Science and Business Media, 2006.
Klimko, E. (1972). An Algorithm for Calculating Indices in Faà di Bruno’s Formula. Retrieved May 22, 2020 from: https://www.stat.purdue.edu/docs/research/tech-reports/1-527/tr-277.pdf
Johnson, W. The Curious History of Faà di Bruno’s Formula. The American Mathematical Monthly Volume 109, 2002 – Issue 3.
Jordan, C. Calculus of Finite Differences, 3rd ed. New York: Chelsea, p. 33, 1965.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 50, 1997.
Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, pp. 35-37, 1958.