What is the Bessel Function?
Bessel functions (named after the astronomer F.W. Bessel) are solutions to differential equations:
Where:
- n is a non-negative real number.
Function values don’t usually have to be calculated by hand; They can be found in many tables (like these Bessel tables).
The solutions are called Bessel functions of order n or—less commonly—cylindrical functions of order n. They are one of the most widely used functions in applied mathematics and are popular in problems that involve circular or cylindrical symmetry, so are sometimes called cylinder functions. They are also important in the study of wave propagation.
Solutions to Bessel’s Equation
Bessel’s equation is a second-order differential equation with two linearly independent solutions:
- Bessel function of the first kind,
- Bessel function of the second kind.
Bessel Function of the first kind

Bessel functions of the first kind (sometimes called ordinary Bessel functions), are denoted by Jn(x), where n is the order.
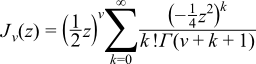
Bessel Function of the second kind
The second solution (Yv or Nv) is called a Bessel Function of the second kind and is denoted by nn(x). It can also be expressed as a Neumann function:
![]()
Uses
A large number of fields use Bessel functions, including:
- Acoustic theory,
- Electric field theory,
- Hydrodynamics,
- Nuclear Physics,
- Radio Physics.
History
Although the functions are named after Bessel (1824), they appear in much earlier work, including:
- Euler’s 1760’s work on vibrations of a stretched membrane,
- Fourier’s 1822 theory of heat flow in spherical bodies.
Bernoulli (1703) solved a differential equation by an infinite series, which is largely regarded as the first time the functions appeared in print. It was Bessel, however, who studied the functions in detail while investigating the elliptic motion of planets.
Hankel Function
The Hankel function is a complex-valued solution to Bessel’s differential equation. These functions are very useful for problems involving spherical and cylindrical wave propagation.
It is also called a Bessel function of the third kind, or a Weber Function.
In essence, a Hankel Function is a combination of Bessel functions of the first kind and second kind. So you can think of it as a “type” of Bessel function. In many mathematical programs, the Hankel is defined in terms of the Bessel. For example, in MATLAB, the Hankel function syntax is:
- First Kind: H = besselh(nu,Z),
- First or Second Kind: H = besselh(nu,K,Z).
Where:
- k = each element (1 or 2) of the complex array z,
- nu = the order of the Hankel function. This must be the same size as Z, or one can be scalar. For example, besselh(4,Z).
As far as evaluating the function, you’re probably going to want to use software, because it is notoriously difficult to evaluate numerically by hand, especially for large order and large argument (Jentschura, 2011).
Hankel Function of the First Kind
The Hankel function of the first kind is defined as:
![]()
Where:
- Jn(z) = Bessel function of the first kind,
- Yn(z) = Bessel function of the second kind.
Contour Integral Definition
The Hankel function can also be represented by the following contour integral:
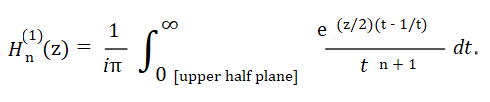
Real Life Applications
Bessel function theory (and the associated Hankel functions) have many real life applications, including:
- Acoustics,
- Atomic and nuclear physics,
- Hydrodynamics,
- Radio physics.
References
Arfken, G. Hankel Functions. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 604-610, 1985.
Bessel, F. (1825). Uber die Berechnung der geo-graphischen Längen und Breiten aus geodätischen Vermessungen (The calculation of longitude and latitude from geodesic measurements), Astronomische Nachrichten, 4, 241-254.
Dublin Institute of Technology. Table of Bessel Functions. Retrieved 1/2/2017 from: http://www.electronics.dit.ie/staff/akelly/bessel-tables.pdf.
Euler, L. (1766). De motu vibratorio tympanorum, Novi Commentarii academiae scientiarum Petropolitanae. 10, 1766, pp. 243-260.
Fourier, M. 1822. Theorie Analytique De La Chaleur.
Jentschura, U. Numerical calculation of Bessel, Hankel and Airy functions. Retrieved November 30, 2019 from: http://arxiv-export-lb.library.cornell.edu/pdf/1112.0072
Korenev, B. (2002). Bessel Functions and Their Applications. CRC Press.
Mathworks. Besselh. Retrieved November 30 from: https://www.mathworks.com/help/matlab/ref/besselh.html
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 623-624, 1953.