A sinusoidal function (also called a sinusoidal oscillation or sinusoidal signal) is a generalized sine function. In other words, there are many sinusoidal functions; The sine is just one of them.
Formula for a Sinusoidal Function
A sinusoidal function can be written in terms of the sine (U. Washington):
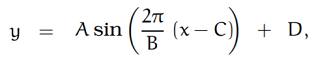
Where A, B, C, D are fixed constants and A & B are positive.
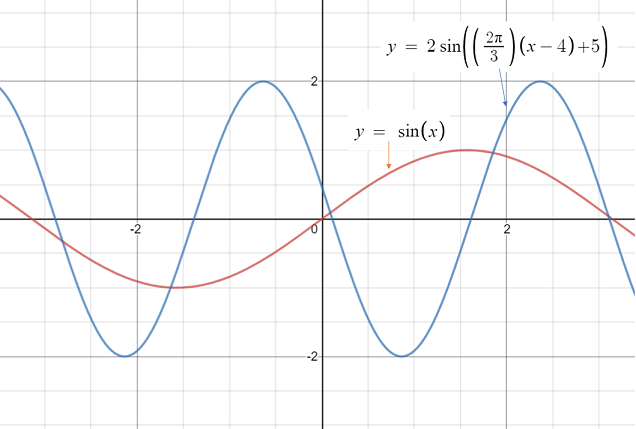
One of the main differences in the graphs of the sine and sinusoidal functions is that you can change the amplitude, period, and other features of the sinusoidal graph by tweaking the constants. For example:
- “A” is the amplitude.
- “B” is the period, so you can elongate or shorten the period by changing that constant.
- “C” is the phase shift (the horizontal shift).
- “D” is the vertical shift. The line y = D – A is where the graph is at a minimum, and y = D + A is where the graph is at a maximum.
Tip: Access the sin vs sinusoidal graph I created on Desmos.com and play around with the different constants to see what each does to the graph.
Alternatively, a sinusoidal function can be written in terms of the cosine (MIT, n.d.):
f (t) = A cos(ω t – Φ).
Where:
- A = amplitude (maximum displacement or distance)
- Φ = phase lag (commonly defined as the delay of the waveform relative to another, but here it’s the value of ωt at the maximum point on the graph)
- ω = angular frequency.
References
AzimaDLI, (2009). The Concept of Phase from: http://azimadli.com/vibman/theconceptofphase.htm
MIT. Sinusoidal Functions. Retrieved December 22, 2019 from: https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-i-first-order-differential-equations/sinusoidal-functions/MIT18_03SCF11_s7_1text.pdf
U. of Washington. Chapter 17. Sinusoidal Functions. Retrieved December 22, 2019 from: https://sites.math.washington.edu/~m124/source/supps/sinusoidal.pdf