Contents:
Binomial Series
The binomial series is a type of Maclaurin series for the power function f(x) = (1 + x)m. You can find the series expansion with a formula:
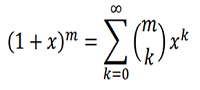
Binomial Series vs. Binomial Expansion
The “binomial series” is named because it’s a series—the sum of terms in a sequence (for example, 1 + 2 + 3) and it’s a “binomial”— two quantities (from the Latin binomius, which means “two names”). The two terms are enclosed within parentheses. For example (a + b) and (1 + x) are both binomials. When these quantities are raised to power and expanded, we get a binomial expansion:
- (a + b)0 = 1
- (a + b)1 = a + b
- (a + b)2 = (a + b) * (a + b) = a2 + 2ab + b2
Once you get above the fourth power, the algebra becomes tedious. You don’t have to calculate these out completely though: there’s a shortcut of sorts. The formula gives the expansion of any binomial series, but you’ll still have to work through some algebra to actually expand it.
Expressing a Function as a Binomial Series
The formula for expanding a binomial series can also be used to simplify more complex functions. The Σ in the formula is summation notation, which basically means to “add everything up”. The (m k) is the binomial coefficient, equal to m! / (k! (m – k)!), where the ! symbol is a factorial.
Example question: Express the following function as a binomial series:

Solution:
Note that the square root in the denominator can be rewritten with algebra as a power (to -½), so we can use the formula with the rewritten function (1 + x)-½
Step 1Calculate the first few values for the binomial coefficient (m k). What you’re looking for here is a pattern for some arbitrary value for “k”. So, you’ll have to work the algebra until you can clearly see a pattern. The first two values for the expansion are:
- -½!/(0!(-½-0)!) = 1
- -½!/(1!(-½-1)!) = -½
These don’t give much of a clue, so let’s continue to the third and fourth terms:
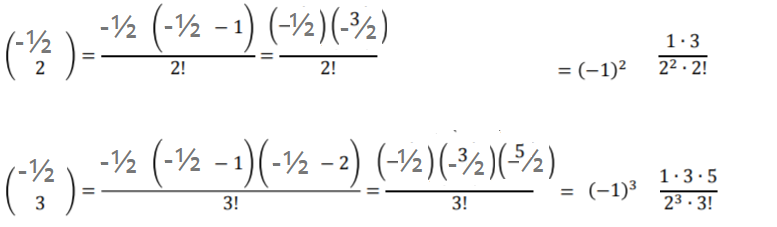
A pattern is emerging, so we can generalize the expansion for any “k”, to:
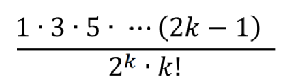
Note: If you don’t see the pattern, continue with finding coefficients until you do! A pattern will nearly always emerge after the third of fourth binomial coefficient, so if you don’t have a pattern by then—go back and check your algebra.
Step 2: Write the solution.
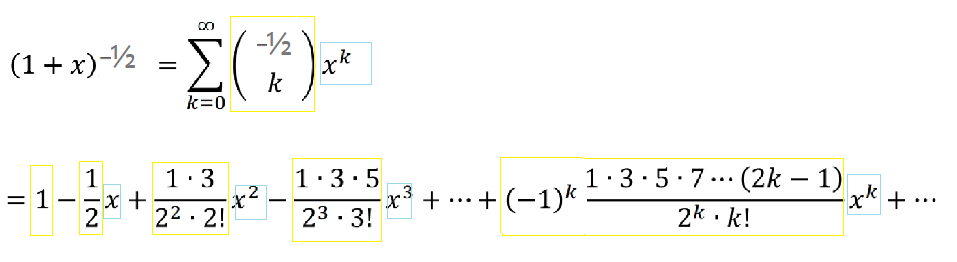
All you’re doing here is writing out the terms you calculated in Step 1 (shown in the yellow boxes), followed by the corresponding power of x (blue boxes).
Convergence of The Binomial Series
The ratio test can be used to show that the series converges for absolute values of x less than 1, |x| < 1 (to the expected sum (1 + x)k) and diverges for |x| > 1. In addition, the radius of convergence is R = 1, unless the exponent (k) is a positive whole number.
Fun Fact: the binomial series formula is inscribed on Newton’s gravestone (at his request) at Westminster Abbey (Nitecki, p. 367).
Binomial Function
The term “binomial function” can mean a few different things:
- A general type of function with two terms, used in calculus and algebra,
- A specific type of function, sometimes defined in terms of a power series,
- The binomial distribution function, used in probability,
- A function used in mathematical software to calculate binomial probabilities.
1. A Binomial Function of Two Terms
“A” binomial function is a function with two terms (Dick & Patton, 1992). Examples:
- f(x) = 2x + 2
- f(x) = 3x2 + 2x.
2. The Binomial Function
“The” binomial function is a specific function with the form:
fm(x) = (1 + x)m
Where “m” is a real number. If m is positive, the function is a polynomial function.
Other forms of binomial functions are used throughout calculus. For example, as a power series expansion, the binomial function is defined for any real number α:
(1 + t)α = eα log ( + t)
Binomial Probability Function
In probability and statistics, The Binomial Probability Function is sometimes just called the binomial function.
The generic form of the binomial probability function is:
Pq(n) = qn(1 – q)N-n
Where “p” is the probability of a success and q is the probability of failure, defined for the set {0,…, N).
“Successes” and “Failures” are defined by what experiment you’re performing, not by success or failure of the entire experiment. For example, if you’re trying to find the probability of picking a red ball from a jar of red and black balls, your “success” would be pulling out a red ball and a “failure” would be pulling a black.
Use in Mathematical Software
Binomial functions are used in software to calculate binomial probabilities. For example, in R, dbinom(x,n,p) finds the number of successes for a certain number of trials.
What is the Gauss Hypergeometric Function?
The Gauss hypergeometric function (sometimes called the Euler-Gauss hypergeometric function or “the” hypergeometric equation) is a special function defined by the series:
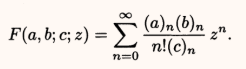
Where:
- F (a, b; c; z) is the hypergeometric function.
- a, b, and c are parameters (reals),
- z is a variable in the complex plane.
As the function is defined by a series, it is sometimes called the hypergeometric series. A similar function, the confluent hypergeometric function, is denoted with F (a; b; z).
The function can also be represented by integrals:
![]()
Calculation
Calculation for anything but the simplest of hypergeometric functions is difficult, especially when all the parameters are complex. This is, in part, because of issues with cancellation and round off error.
What is the Gauss Hypergeometric Function Used For?
The function is an analytic function that generates more complex combinatorial numbers, which generalize the binomial series. The function provides information about the relationships between combinatorial numbers and their growth.
Many special functions can be expressed in terms of the hypergeometric. Closed form solutions of linear differential equations with polynomial coefficients can many times be defined in terms of Gauss’s hypergeometric function.
The Gauss Hypergeometric Function function arises in many practical areas, like:
- Binary stars (where two stars orbiting around a common center of mass),
- Mathematical finance (an interdisciplinary study of financial markets),
- Photon scattering from atoms,
- Networks,
- Non-Newtonian fluids (a fluid with variable viscosity is depending on applied stress or force).
References
Bolton, W. (2000). Mathematics for Engineering. Newness.
Dick, T. & Patton, C. Calculus, Volume 1. PWS-Kent Publishing Company.
Farahmand, A. 11.10 More About Taylor Series; Binomial Series. Retrieved September 22, 2020 from: https://math.berkeley.edu/~arash/notes/07_01.pdf
Gonzalez-Zugast, J. (2011). The Binomial Series. Retrieved September 23, 2020 from: http://faculty.uml.edu/jennifer_gonzalezzugasti/Calculus%20II%20Video%20Lectures/documents/9.10.1TheBinomialSeries.pdf
Nagy, G. Binomial functions and Taylor series (Sect. 10.10). Retrieved December 19, 2019 from: https://users.math.msu.edu/users/gnagy/teaching/12-spring/mth133/L35-133.pdf
Nitecki, Z. (2009). Calculus Deconstructed. A Second Course in First-Year Calculus.
Olive, J. (2003). Maths: A Student’s Survival Guide: A Self-Help Workbook for Science and Engineering Students. Cambridge University Press.
Taubes, C. (2010). Lecture notes on probability, statistics and linear algebra. Retrieved December 19, 2019 from: http://people.math.harvard.edu/~knill/teaching/math19b_2011/handouts/chapters1-19.pdf