- What is Extrapolation?
- What is Interpolation?
- Real Life Uses
- Use in Statistics
- Other Practical Uses
- Cautions with Use of Interpolation and Extrapolation
- Interpolation Functions
What is Extrapolation?
Extrapolation is a way to make guesses about the future or about some hypothetical situation based on data that you already know. You’re basically taking your “best guess”. For example, let’s say your pay increases average $200 per year. You can extrapolate and say that in 10 years, your pay should be about $2,000 higher than today.
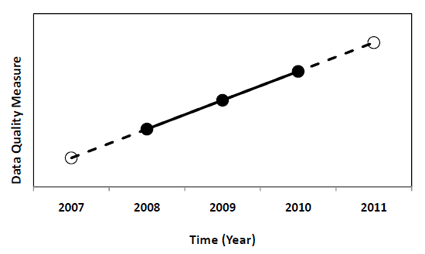
What is Interpolation?
Interpolation allows you to estimate within a data set; it’s a tool to go beyond the data. It comes with a high degree of uncertainty. For example, let’s say you measure how many customers you get every day for a week: 200, 370, 120, 310, 150, 70, 90. According to that number, you should get just under 10 customers per hour (1,310 customers/ 168 hours in a week). Let’s say you staff your business 24-7 to deal with those hourly customers. You’re probably going to get zero customers at night and on the weekends, therefore wasting resources. (Note: a better way to figure out peak times is the Poisson Distribution).
In calculus, the art of interpolation has largely been lost, as it has been replaced with numerical methods like the Gregory-Newton formula. Historically, interpolation goes back to ancient times as a method for estimation. Exact methods were developed by Thomas Harriot (1560-1621) and Henry Briggs (1561-1630) of Briggs logarithm fame; Newton, Leibniz, and Gregory began their work with interpolating, leading to the discovery of the binomial theorem and Taylor’s theorem (Stillwell).
Real Life Uses of Extrapolation
You extrapolate to some degree in your daily life. For example, you might look forward to your monthly paycheck and you assume that you’re going to get it based on known data (the fact that you’ve got paid monthly, on-time for the last year). But what if your company goes bankrupt? Or the market crashes? Or the bank mistakenly freezes your bank account? In this particular case, extrapolation has a fair amount of certainty (you’re probably going to get your paycheck), but that isn’t always the case.
Use of Extrapolation in Statistics
Extrapolation can mean several things in statistics, but they all involve assumption and conjecture (extrapolation is far from an exact science!):
- The extension of a statistical method where you assume similar methods will be used.
- The projection, extension, or expansion of your known experience into an area that you do not know or that you haven’t experienced yet.
- The use of equations to fit data to a curve. You then use the equation to make conjectures. This is known as curve fitting or regression, which can get quite complex, with the use of tools like the Correlation Coefficient.
Other Practical Uses of Extrapolation
Extrapolation is used in many scientific fields, like in chemistry and engineering where extrapolation is often necessary. For example, if you know the current voltages of a particular system, you can extrapolate that data to predict how the system might respond to higher voltages.
Cautions with Use of Interpolation and Extrapolation
In general, you should extrapolate with caution. For example, you might be able to rely on a steady paycheck coming in for a few months or years, but it probably wouldn’t be a good idea to assume that same company is going to be still paying you 20 years down the road!
Interpolation Function
An interpolation function (or interpolant) approximates a function using a set of known, discrete points (also called nodes or interpolation points). For example, you can use an interpolation function to interpolate values given in a table.
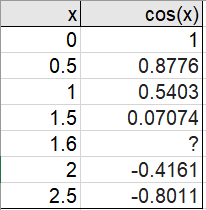
The resulting function can be used to describe the function at every point in space.
Interpolation is used to interpolate values from computations. It can also be used to develop schemes for numerical integration and numerical differentiation.
Interpolation Function vs. Fitting Function
An interpolation function passes through all of the known points. In contrast, a fitting function doesn’t have to pass through all of the points— it can simply find the line that fits the best (Xue & Chen, 2008).
Types of Interpolation Function
- Bulirsch-Stoer: Fits a polynomial function or rational function; Provides solutions of ordinary differential equations.
- Cubic spline: Fits a different cubic function between each pair of known points.
- FFT: Calculates the Fourier transform of a vector containing values of a periodic function, then calculates the inverse Fourier transform with more points.
- Lagrange Interpolating Polynomial: Fits a Lagrange polynomial—a linear combination of n degree n – 1 polynomials, where each equals zero at exactly n – 1 points (Dedford, 2020).
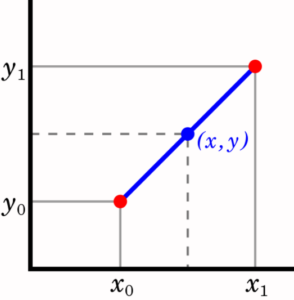
- Linear : fits a linear function to the points.
- Nearest neighbor: the value of an interpolated point is set to the value of its nearest known neighbor.
- Neville: interpolates a function at a given point with increasingly higher order Lagrange interpolation polynomials (Mitchell, 2020).
- Newton: Fits a polynomial function to “difficult” functions; allows for incremental interpolation (Verschelde, 2018).
References
Dedford, D. (2020). Lagrange Interpolation. Retrieved September 5, 2020 from: https://people.csail.mit.edu/ddeford/Lagrange_Interpolation.pdf
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Mitchell, K. (2020). Neville’s Method. Retrieved September 5, 2020 from: http://people.math.sfu.ca/~kevmitch/teaching/316-10.09/neville.pdf
Stillwell, J. Mathematics and Its History. 3rd Edition. Springer.
Verschelde, J. (2018). MCS 471 Lecture 7(b). Newton Interpolation. Numerical Analysis. Retrieved September 5, 2020 from:
Westerink, J. (2018). Lecture 2: Introduction to Interpolation. Retrieved September 5, 2020 from: https://coast.nd.edu/jjwteach/www/www/30125/pdfnotes/lecture2__5v14.pdf
Xue, D. & Chen, Y. (2008). Solving Applied Mathematical Problems with MATLAB. CRC Press.