Contents (Click to skip to that section):
See also: Sum of a Convergent Geometric Series.
What is an Infinite Sequence?
An Infinite Sequence (sometimes just called a sequence) is a function with a domain of all positive integers. In beginning calculus, the range of an infinite sequence is usually the set of real numbers, although it’s also possible for the range to include complex numbers.
Infinite Sequence Formula
The general form of an infinite sequence is
f(1), f(2), f(3),…f(n),…
Where:
- … = “Goes on and on until infinity,”
- n = a positive integer (the input),
- f(n) = a real number (the output).
An alternate notation uses subscripts:
a1, a2, a3,…an,…
The meaning is the same: For example, a1 is equivalent to f(1).
Examples
A simple example of an infinite sequence is 1, 4, 9, 16, 25, …. The elements here (a.k.a. the range) are called the terms of the sequence.
Note that you can’t just write down a list of numbers and call it a “sequence”. It has to be a function. That is, there must be some kind of pairing between the inputs (the positive integers in the domain) and outputs (the real numbers in the range). In the simple example above, the pairing is “x squared”:
- 12 = 1,
- 22 = 4,
- 32 = 9,
- 42 = 16,
- 52 = 25.
and so on.
Order makes a difference with an infinite sequence. For example, you can reorder the list:
2, 4, 8, 16, 32, …
as
2, 8, 4, 16, 32,…
Which makes two different infinite sequences.
Limit of an Infinite Sequence
An infinite sequence has a limit if the nth term (an) converges to a constant L as n gets very large. As a formula, that’s:
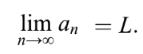
If the terms don’t approach a limit, the sequence diverges.
An infinite sequence with one term repeated has that term as limit. This sounds obvious, but it’s one property of infinite limits that becomes important in mathematical theory (for example, in topology).
Infinite Geometric Sequence
A geometric sequence is one where the common ratio is constant; an infinite geometric sequence is a geometric sequence with an infinite number of terms. For example:
- 4, 12, 36 is a geometric sequence (each term is multiplied by 12, so r = 12),
- 4, 12, 36,… is an infinite geometric sequence; the three dots are called an ellipsis and mean “and so forth” or “etc. etc. etc.”
What is an Infinite Series?
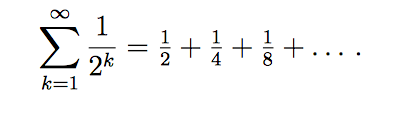
An infinite series (also called an infinite sum) is a series that keeps on going until infinity. For example, 1 + 1 + … or 1 + 2 + 3 +…. In notation, it’s written as:
a1 + a2 + a3 + ….
The dots (or ellipsis) mean that the number of terms are infinite.
Obviously, if you have an infinite number of terms, it would be impossible to actually write out those terms (it would take you an infinite amount of time!), so summation notation is usually preferred:
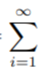
Why are Infinite Series Useful?
Infinite series are useful for finding approximate solutions when a problem can’t be expressed in terms of a known function, or where there isn’t a closed-form or exact solution. For example, many differential equations don’t have solutions of known functions or elementary functions; Those solutions can be expressed as infinite series (Bach, 2018).
Convergent and Divergent Infinite Series
While some infinite series have a sum (i.e. they converge to a certain numerical value), many diverge and fail to converge to a finite numerical value. In these cases, the values are found with the limit of partial sums.
- If the limit exists for a particular sequence of partial sums, then the series is convergent.
- If the limit of partial sums doesn’t exist, the series is divergent.
In summation notation, this can be written as (Berkeley):
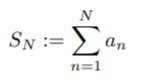
For example, you could add up the first 3 terms, or the first 10. For the simple series 1 + 2 + 3 +…, this would give:
- 1 + 2 + 3 = 6
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.
There are other ways to test for convergence. For example, Abel’s Test allows you to define convergence or divergence by the types of functions contained in the series.
Infinite Arithmetic Series
An infinite arithmetic series is the sum of an infinite (never ending) sequence of numbers with a common difference.
An arithmetic series also has a series of common differences, for example 1 + 2 + 3. Where the infinite arithmetic series differs is that the series never ends: 1 + 2 + 3 …. The three dots (an ellipsis) means that the series goes on and on to infinity.
A couple of examples of an infinite sequence:
2, 4, 6, 8, … or 1, 5, 10, 15, … (notice the commas)
An infinite series has either addition or subtraction symbols with a common difference:
2 + 4 + 6 + 8, … or 1 – 5 – 10 – 15, …
It’s also possible (and actually quite common) to have subtraction and addition in the same series.
Summation Notation for Infinite Arithmetic Series
You can use summation notation for infinite arithmetic series. Instead of writing out a series of additions or subtractions, you use a sigma symbol to denote the summation. For example, the following infinite series is in multiples of 4, beginning with the second multiple.
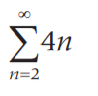
You can tell it’s an infinite series because of the infinity symbol for one of the bounds (the numbers on top or bottom of the summation symbol).
Divergence of Infinite Arithmetic Series
Every infinite arithmetic series is divergent. These series will never converge, tending either to positive infinity, negative infinity, or an oscillating number. For example:
- The sum of all natural numbers 1 + 2 + 3 +… is divergent to ∞.
- The series -1 -1 -1 -… is divergent to -∞.
- The series 1 – 1 + 1 – 1 + 1 + … oscillates (and therefore diverges).
There is one exception: the infinite arithmetic series 0 + 0 + 0 + … converges to zero.
As any infinite arithmetic series always diverges, it isn’t possible to calculate their sums, because you would be infinitely adding (or subtracting) the same amount.
Infinite Geometric Series
A “series” is just the sum of a sequence; The sum of terms of an infinite geometric sequence is called an infinite geometric series.
The general form of an infinite geometric series is
a1 + a1r + a1r2 + a1r3 + …,
Where:
- a1 = the first term,
- r = the common ratio.
Sum of an Infinite Geometric Series
An infinite geometric series will only have a sum if the common ratio (r) is between -1 and 1. That’s because if r is greater than 1, the sum will just get larger and larger, never reaching a set figure. So you could say that all of infinite geometric series sum up to infinity, with the exception of those that have a common ratio of between -1 and 1. That helps with calculation: anytime you have one of these series that has a large r, then you know it will sum to infinity. Otherwise, you’ll need to work a relatively simple formula.
The formula is:
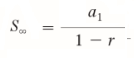
Where:
- a1 = the first term in the series,
- r = the common ratio of the series, which is the amount between each number.
The formula is only valid if |r| < 1, which can be written equivalently as -1 < r < 1. In other words, if r is between -1 and 1, then the series has a sum.
Examples
Example Question: Does the infinite geometric sequence 2, 4, 8,… have a sum?
Solution:
Step 1: Find “r”, the common ratio. Each number is multiplied by 2 in this sequence (8 / 4 = 2), so r = 2.
There’s no need to go any further: 2 is not between -1 and 1, so this sequence doesn’t have a sum.
Example question 2: Does the sequence 4, 1, ¼ … have a sum?
Step 1: Find “r”, the common ratio. Each number in the sequence is multiplied by ¼ (¼ / 1 = ¼), so this sequence does have a sum.
Step 2: Insert your values into the formula. For this sequence, r = ¼ and the first term is 4, so:
S∞ = 4 / (1 – ¼ ) = 16/ 3 = 5.3333.
Infinite Sequence
A cause of some confusion is that there is also an Infinite Sequence. While it sounds similar, it’s actually a completely different concept. While you add the terms of series, a sequence is a list of terms. For example:
- Infinite Series: 1 + 2 + 3 + …
- Infinite Sequence: 1, 2, 3, …
Note that you can’t just write down any list of numbers and call it a “infinite sequence”. It has to be a function; In other words, the terms have to be related in some way so that the inputs and outputs are related.
References
Aufmann, R. et al. (2007). College Algebra. Cengage Learning.
Bach, B. (2018). A Student’s Guide to Infinite Series and Sequences. Cambridge University Press.
Berkeley. Infinite Series. Retrieved July 1, 2020 from: https://math.berkeley.edu/~scanlon/m16bs04/ln/16b2lec25.pdf
Chug, O. & Parkash, K. (2005). Comprehensive Advanced Calculus: Paper 1. Laxmi Publications.
Grigorieva, E. (2016). Methods of Solving Sequence and Series Problems. Birkhäuser.
Heathcote. C. (2012). Probability: Elements of the Mathematical Theory. Courier Corporation.
Karr, R. et al. (2014). Intermediate Algebra: A Guided Approach. Cengage Learning.
Swokowski, E. (1979). Calculus with Analytic Geometry. Taylor & Francis.
Tussy, A. & Gustafson, R. (2012). Intermediate Algebra. Cengage Learning.