Contents:
What is a Series Expansion?
A series expansion is where a function is represented by a sum of powers of either:
- One of its variables,
- Another function (usually an elementary function).
For example, the natural exponential function ex can be expanded into an infinite series:
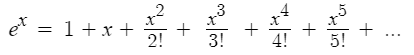
This particular expansion is called a Taylor series.
Series expansions have a myriad of uses in a vast array of scientific areas. For example, in calculus, if you know the value of a function at a certain point (and its derivatives), you can calculate values for the whole function. Or, if you have a particularly ugly derivative or integral, you can use a series expansion to simplify the math and find an approximate solution.
General Types of Series Expansion
The most common series expansions you’ll come across are:
- Binomial series: Two binomial quantities are raised to a power and expanded. For example, (a + b)2 = (a + b) * (a + b).
- Power series: Like a polynomial of infinite degree, it can be written in a few different forms. A basic example if 1 + x + x2 + … + xn.
- Taylor & Maclaurin Series: approximates functions with a series of polynomial functions.
- Laurent series: a way to represent a complex function as a complex power series with negative powers.
These aren’t the only tools for series expansion though. Many others exist, but they tend to be used in very specific circumstances. For example, Zernike polynomials are used in optics to calculate the shape of aberrated wavefronts in optical systems (Indiana, 2020) and Stirling series are used for approximating factorials. Others include:
- Arctangent series expansion:
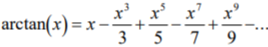
- Dirichlet series: Any series of the form
 . The Reimann zeta function is a famous example (McCarthy, 2018).
. The Reimann zeta function is a famous example (McCarthy, 2018). - Legendre functions of the first kind (also called Legendre polynomials), are solutions to the Legendre differential equation.
- Puiseux series: a generalization of power series that allows for negative and fractional exponents of the indeterminate T.
Arctangent Series Expansion
The arctangent function can be expanded as a Maclaurin series:

The arctangent series expansion is derived by taking the basic integral [1]:
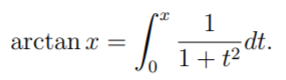
The integrand is then replaced with the series:
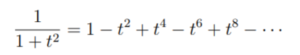
Finally, each term is individually integrated to give the series (for -1 < x < 1). Note that both sides equal zero when x = 0, so there’s no “+ C”.
Although the series is usually attributed to Gottfried Leibniz (1646-1716) or James Gregory (1833 to 1675) [2], it was known two centuries earlier to Indian mathematician Nilakantha Somayaji (ca. 1444–1544) [2].
Why is the Arctan Series Expansion Important?
Perhaps the most widespread us of the arctangent series is as an approximation for π. As well as the ratio of a circle’s circumference to its diameter, π is also defined as twice the least positive x for which cos(x) = 0.
Depending on the author, there are between 2 and 11 terms for the series expansion. More terms doesn’t necessarily mean more accuracy: Machin’s two term series approximates π as 3. 157866845 and Dodgson’s 11 term series gives π as 3.077143544 [3].
Another reason for having an interest in the arctan series is purely for historical interest. The history of this particular series is important because it was developed pre-calculus; It demonstrates early ideas on series and how they connect with quadrature or processes for finding the area under a curve (a.k.a. integration) [4].
Arctan Series Expansion: References
[1] 2.3 Computing Pi (continued). Retrieved April 6, 2021 from:
https://www.macalester.edu/aratra/chapt2/chapt2_3a.html
[2] Hwang Chien-Lih. (2004). Some observations on the method of arctangents for the calculation of π. The Mathematical Gazette. The Mathematical Association.
[3] Abeles, F. Charles L. Dodgson’s Geometric Approach to Arctangent Relations for Pi. Historia Mathematica 20, pp. 151-159. Retrieved April 6, 2021 from: http://users.uoa.gr/~apgiannop/Sources/Dodgson-pi.pdf
[4] Roy, R. (1990). The Discovery of the Series Formula for π by Leibniz, Gregory and Nilakantha. Retrieved April 6, 2021 from: http://users.uoa.gr/~apgiannop/Sources/Roy-pi.pdf
Common Series Expansions


References
Indiana University Bloomington. (2020). Standards for Reporting the Optical Aberrations of Eyes. Retrieved July 10, 2021 from: https://www.opt.indiana.edu/vsg/library/vsia/vsia-2000_taskforce/tops4_2.html#:~:text=Standards%20for%20Reporting%20the%20Optical%20Aberrations%20of%20Eyes&text=The%20Zernike%20polynomials%20are%20a,pupil%20of%20an%20optical%20system.
McCarthy, J. (2018). Dirichlet Series, Retrieved December 2, 2020 from: https://www.math.wustl.edu/~mccarthy/amaster-ds.pdf
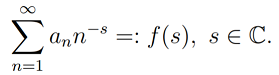 . The
. The