Calculus Definitions > Double Integral in Statistics
Contents:
What is a Double Integral in Statistics?
A double integral(∬) is a way to integrate over a two-dimensional area. While it’s not very common to come across a double integral in statistics, you might come across them in applied statistics — especially in the sciences.
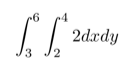
Just as an ordinary integral allows you to find the area under a curve, a double integral helps you to find the volume under a two-dimensional area or a surface. The following picture shows the volume under the surface z = 10 – (x2-y2)/8.

Solving a Double Integral
Solving this type of integral is not as difficult as it looks. The general steps are:
- Solve the inner integral. Start by drawing in some brackets so you can easily visualize the integral’s nested structure.
- Substitute that result into your equation,
- Solve the outer integral.
You can actually get the same answer by changing the order in which you integrate. The math you need to go through will be different, but the answer will be the same.
Simple Example: Double Integrating a Constant Function
The simplest of double integrals is the double integral of a constant function. Here, the integral will be equal to the product of the constant and the measure of the domain of integration.
Suppose f(x,y) = 2, and set our domain as:
![]()
Then we can write our double integral as
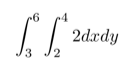
And analyze it using the method above:
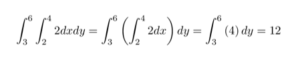
The answer to this, 12, is the area of the domain times the constant of integration, 2. We can generalize this: when finding the double integral of any constant function c, the solution will always be the area of the region times c if the domain is in R2.
References
Oregon State Calculus Quest Study Guide. Double Integrals. Retrieved from https://math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/vcalc/255doub/255doub.html on July 27, 2019.