Two functions can be combined to make a new function through the basic arithmetic operations addition, subtraction, multiplication and division.
The following arithmetic rules show you what happens when you combine two functions f(x) and g(x).
- Sum: (f + g)(x) = f(x) + g(x)
- Difference: (f – g)(x) = f(x) – g(x)
- Product: (f · g)(x) = f(x) · g(x)
- Quotient: (f / g)(x) = f(x) / g(x); note that the quotient f/g isn’t defined when g(x) = 0 because of division by zero.
The new functions are called an arithmetic combination of functions. The domain for the new function is all real number common to the domains of f(x) and g(x), with the exception of the quotient, where x cannot equal zero.
Arithmetic Combinations of Functions: Examples
Example question #1: Find (f + g)(2) for the following two functions:
- f(x) = x2 + 3x – 7
- g(x) = 4x + 5 at x = 2.
Solution: (f + g)(2) = f(2) + g(2) = 3 + 13 = 16.
Example question #2: Find the quotient of the functions f(x) = x2 + 3x – 7 and g(x) = 4x + 5 at x = 3.
Solution: (f / g)(3) = f(3) / g(3) = 11 / 17.
Example question #3: Find (f · g)(x) for the following two functions:
- f(x) = 3x + 4
- g(x) = 2x2 – 1.
Solution: We aren’t given an x-value here, so in order to combine these functions, substitute every value of x in f(x) = 3x + 4 with g(x) = 2x2 – 1:
3(2x2 – 1) + 4.
Expanding the expression gives the solution:
6x2 + 1.
Graphical Solutions
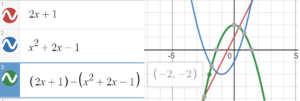
If algebra isn’t your forte, you can use your graphing calculator to get a very good approximation for a difference of two functions. For example, let’s say you wanted to find the difference at x = 2 of
- f(x) = 2x + 1
- g(x) = x2 + 2x – 1
Algebraically, the rule is: (f – g)(x) = f(x) – g(x), which gives us:
(2(2) + 1) – (22 + 2(4) – 1) = 5 – 7 = -2.
You can find the same solution on a graphing calculator by graphing three functions:
- f(x)
- g(x)
- f(x) – g(x)
I used Desmos.com to graph the functions; The solution at x = 2 (the green graph is #3 the difference function) is highlighted: