The arcsin function, y = arcsin(x), is “the angle with sin x.”
It is the inverse function to y = sin x, restricted to the interval -π /2 ≤ x ≤ π /2.
“Arcsin” is the abbreviation for arcsine and is occasionally also designated by sin-1x. Since this can be confused for a multiplicative inverse (a reciprocal), it is generally suggested to avoid that notation. In computer programming languages, where every letter counts, arcsin is often abbreviated further to asin.
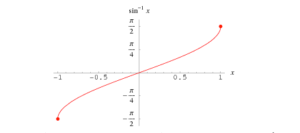
The Graph of Arcsin
The graph of the arcsin looks like a piece cut out of the graph of sine, and flipped.
Applications of the Arcsin Function
The inverse trigonometric functions are important in engineering, navigation, physics, and geometry because, given an angle’s trigonometric ratios, they can tell us what the angle is. In particular, the angle of a right triangle would be given by the arcsin of the ratio of the opposite side to its hypotenuse.
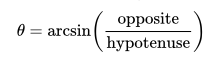
If both opposite (o) and adjacent (a) sides are known but not the hypotenuse, the Pythagorean Theorem can be used to substitute the square root of (a2+o2) in the denominator of the above equation.
Suppose you know that a roof drops 4 feet and runs out 10. Then you know that the hypotenuse is the square root of 16 + 100 = 116, or about 10.77. The arcsine of (4/10.77) is 21.8 degrees or 0.38 rad.
References
Gelfand & Saul. Trigonometry. pg 209-210. Retrieved from https://books.google.com/books?id=ZCYtwHFVZHgC on August 18, 2019