Conjugate Function

Types of Functions >

A conjugate function is defined as:


This classical optimization tool represents the maximum gap between a function and its slope (Charpentier, 2020). It represents the supremum (assuming one exists) of a family of affine functions (Gorni, 1989).

Conjugate Function: Intuitive Examples

The conjugate function for the negative logarithm f(x) = -log x is (Fu, 2020):

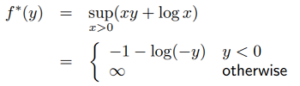
Graphically, the one-dimensional case of a conjugate function is fairly easy to visualize:

1. Graph the function f and slope y.
2. Look along the x-axis to find the point with the maximum distance between the graph of f and the line g(x) = yx.
3. Define a new function with slope y that passes through the point (x*, f(x*)).

For example, the linear function f(x) = x²/ 2 has a derivative of f′ = 2x. The maximum gap between these two functions is at f(2):

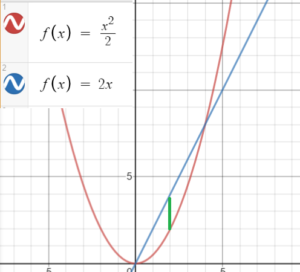
Formal Definition

The following property is used to define a conjugate function:
F*(y) = sup_{x≥0 (xy − f(x)).}
If f: I → ℝ is a convex function defined on interval I, then f*:I*→ denotes the conjugate function given by
f*(y) = supx∈I(xy − f(x)) with domain I* = {y ∈ ℝ: f*(y) < ∞}.

f*(x) is always convex, even if the original function isn’t.

References

Graph of conjugate function: Desmos.com.
Brown, J. & Churchill, R. (1996). Complex variables and applications (6th ed.). New York: McGraw-Hill.
Charpentier, A. (2020). On the conjugate function. Retrieved November 12, 2020 from: https://www.r-bloggers.com/2020/01/on-the-conjugate-function/
Fu, A. (2020). EE364a: Lecture Slides.
Gorni, G. (1989) Conjugation and Second-Order Properties of Convex Functions. Journal of Mathematical Analysis and Applications, 158. pp. 293-315.
Vujanovic, B. & Jones, S. (1989). Variational Methods in Nonconservative Phenomena, Mathematics in Science and Engineering.
Vandenberghe, L. (2019). Conjugate Functions. Retrieved November 12, 2020 from: http://www.seas.ucla.edu/~vandenbe/236C/lectures/conj.pdf