General Functions and Graphs
Asymptotes
Continuous Function / Check the Continuity of a Function
Definition of a Function & Types of Functions
Discontinuous Function: Types of Discontinuity
Domain and Range of a Function
Function Composition: Decomposing a Composite Function
Inverse Function: Definition, Derivative
Logarithm Function: Definition
Polynomial Function: Definition, Examples, Degrees
Rational Function & Proper Rational Function: Simple Definition
Trigonometric Function: Definition, Example
Y-Intercept
X-Intercept: Definition, Example, Finding
Numbers and Variables
Absolute Value
Continuous Variable (Continuous Data)
Factorials
Finite Numbers and Sets
Imaginary Numbers & Complex Numbers
Improper Fraction
Independent and Dependent Variable
Integer & Non Integer
Significant Figures
Scalar
Vector
Geometry and Symmetry
Symmetry of Functions
Even and Odd Functions
Law of Cosines
Law of Sines
Pythagorean Theorem
What is a Finite Number?
A finite number can be measured or counted. For example, the set {1, 2, 3} is finite, and the set {1,2…∞) is not (because you’ll be counting to infinity).
The terms finite and infinite are often confused, particularly in the case of very large numbers. For instance, consider the number of stars in the universe. We do not know exactly how many stars there are, with an estimated 300 billion stars in our galaxy alone. However, if the technology existed to view all of the stars in the universe, the number of stars could conceivably be counted, however large the number. Therefore, the number of stars in the universe is usually considered as finite, not infinite.
Finite Sets of Numbers

{1, 3, 5, 7, 9, 11}
If you begin counting the numbers of the set at 1, by the time you reach 11 we will have run out of numbers to count. This set is a finite set with six elements. In everyday life, there are a whole host of examples of finite sets. For example:
- The alphabet,
- A bag full of bagels,
- Players on a football team,
- Passengers on a train.
Conversely, consider a set of numbers like the following:
{1, 1/2, 1/4, 1/8…]
Here the set starts at one and each proceeding value is decreased by 1/2. The three dots indicate the counting goes on forever; It is possible to continue this process forever with each new value becoming smaller and getting closer to zero. Therefore, this number set is infinite.
Law of Sines
The Law of Sines helps you to find values for missing angles and sides in triangles, is defined as:
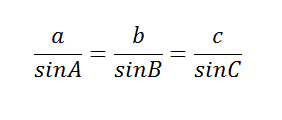
The rule is one of the most useful rules that you’ll need to solve problems that involve triangles.
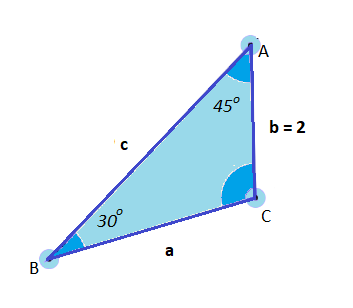
On this triangle, if we only had the values given above, that
- A = 45°,
- B = 30°,
- b = 2,
we could figure out all of the sides and angles.
Solving using the Law of Sines
Using the law of sines involves a little logic. It isn’t quite as easy as plugging some numbers into a formula and solving. You have to look at the information you’re given, and take small steps to solve for the missing pieces.
Probably the easiest place to start with the above image is to solve for the missing side C, because we have the values of the angles A and B. We need one more piece of information—the sum of all angles in a triangles is 180°:

After we do this, we can start calculating the sides. The first side that we’ll solve is side a. The following steps are basically a series of steps for a logic problem. There isn’t one way to do this for all missing sides and all missing angles, but once you’ve worked through a problem or two you should be able to see which parts of the law you’ll need for your particular problem.
Step 1: Find the value of sin(B), which is the sine of 30 degrees. You don’t really “solve” for sin(3). Rather, it’s one of those “useful math facts” you may have learned in trigonometry. Note: the proof of why sin(30) = 0.5 is beyond the scope of this article, but this Dr. Math post does a great job of explaining why that particular math fact is true.
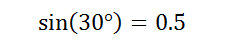
Step 2: Divide, as the law states: b/sin(30°). We know sin(B) from Step 1, so we’re basically cherry picking the part of the law that we know we can solve.
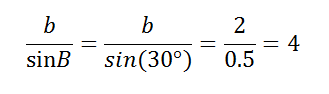
Step 3: Use another part of the law (along with the solution from Step 2) to fill in a blank:
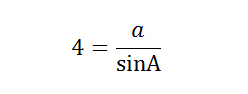
Since we know the value of the angle A, it’s easy to find out the sine. If you use your calculator (I typed “sin 45 degrees” into Google), you’ll see that sin(45° ) is 0.707 (rounded to three decimals).
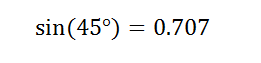
After this, we need to do a little bit of algebra:
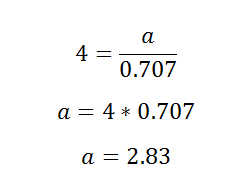
This law is easy to use, and we straightforwardly calculated the length of side a. By using this same process, we can find the length of side c.
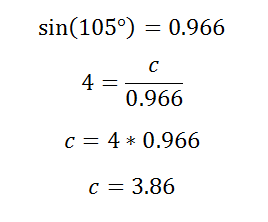
Law of Cosines
Most of the time, we solve the sides of triangles with the use of the Pythagorean theorem. But, it only works for right angled triangles. That’s where the Law of Cosines comes into play; It’s basically the Pythagorean theorem, with a little extra to make it work for all types of triangles.
The formula is:
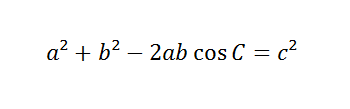
Which is very similar to the Pythagorean theorem:
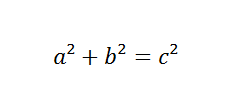
Solving a triangle with the Law of Cosines: Example
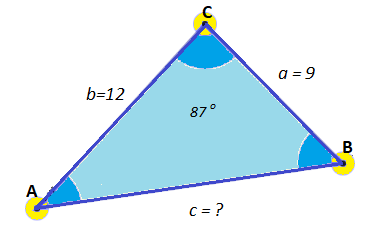
Since the 89 degree angle isn’t exactly 90 degrees, you can’t use the Pythagorean theorem to solve for the missing side C. This means that you’ll need to use the Law of Cosines (which is the case every time you have an angle that isn’t 90 degrees).
Step 1: Put the values that you know (from the question) into the Law of Cosines formula:
- a2 + b2 – 2ab cos C = c2
- 92 + 122 – 2(9 * 12) cos (87°) = c2
- 81 + 144 – 216 * cos (87°) = c2
Step 2: Calculate the value of cos(87°). Tip: If you don’t have a scientific calculator, just type “cos 87 degrees” into Google.
- cos(87°) = 0.05 (to two decimal places).
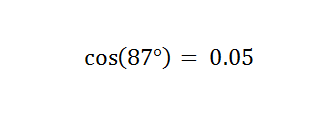
Insert that new piece of information into the formula:
81 + 144 – 216 * 0.05 = c2
Then use algebra/arithmetic to solve for c:
- 225 – 10.8 = c2
- 214.2 = c2
- √214.2 = √c2
- c = 14.6*
*Since you are working with lengths, you only need to take the positive value of the square root.
This will be the length of the side c up to one decimal place.
Finding Angles
Another thing that the Law of Cosines is beneficial for is finding angles, if you know all of the sides. If you rearrange the original formula, you can get all of the angles inside the triangle. Here are the formulas for all individual angles:
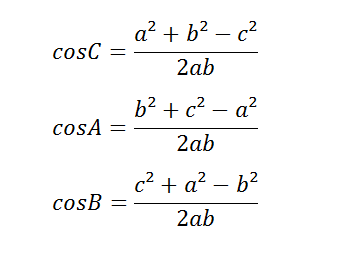
Pythagorean Theorem
Contents:
What is the Pythagorean Theorem?
The Pythagorean theorem tells you the length of a hypotenuse: the longest side of a triangle. Pythagoras concluded that the square of the longest side in a right triangle is equal to the sum of the squares of the other two sides. However, this theorem is based only on right-angled triangles. This means that the triangle must contain one 90° angle for this formula to be used.
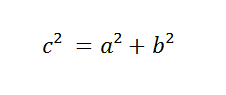
Example
Example question: Find the length of the hypotenuse in this right triangle.
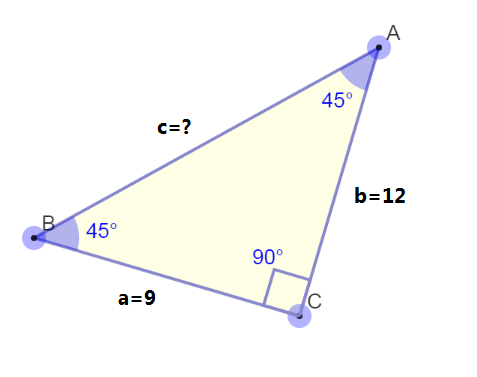
On the triangle above, two sides are given: a = 9, and b = 12. To find the length of c, put in the values of a, and b into the equation. After that, you’ll only need basic arithmetic to solve the equations.
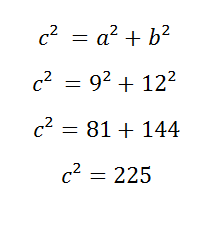
Next, we need to calculate the square root of this equation to get the length.
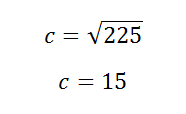
The Pythagorean theorem was known long before the first proof, and it has been proven in many different ways. Some are algebraic, some are geometric, and there is also proof by using calculus.
Proving the Pythagorean theorem with calculus
First, let’s set up the proof.
![JohnBlackburne [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)] proof of pythagorean theorem](https://www.statisticshowto.com/wp-content/uploads/2018/12/pythagorean-proof-2.png)
- The first triangle (ABC) has the hypotenuse shown in yellow. This same side is represented in the second triangle with y (also in yellow).
- Side AC (light green) matches the second triangle’s length x.
- Side AB (dark green) is shown with a length of a.
If we increase the side AC to point D (first triangle) by a minimal amount dx (second triangle), then we would extend the side to the point D. This means that the hypotenuse y will also be extended by a minuscule amount. These increments create a new triangle CDE (shown in red).
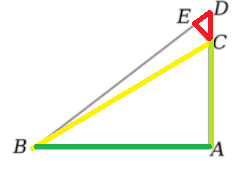
This new triangle CDE is similar to ABC, which means that the ratios of their sides will be the same. Next, let’s set up an equation showing this ratio:
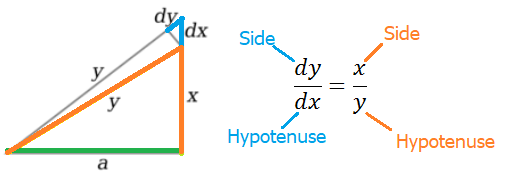
This equation can be reformulated using algebra:
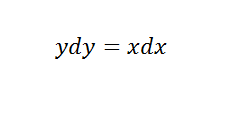
Now, we can use our integration rules to solve it. For this particular differential equation, use the power function rule for integration:
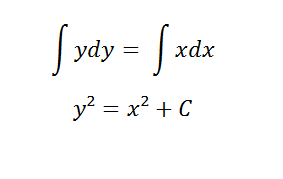
The constant can be deduced if we use an initial condition (x, y) = (0, a):
y2 = x2 + C
0 + a2 = C
a2 = C.
That gives us the equation:
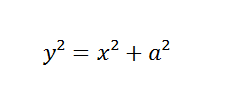
This is exactly the Pythagorean theorem.
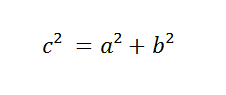
Improper Fraction
An improper fraction is a fraction that has a larger numerator than a denominator. It is written in the form p/q, and p is larger than q.
Examples of improper fractions:
- 6/5,
- 7/8,
- 100/6,
- 3/2.
The following two facts combined mean that an improper fraction will always be greater than 1:
- The equation p/q = 1 means that p = q.
- p/q is less than 1 if p is less than q.
Rewriting an Improper Fraction as a Mixed Number
An improper fraction is just another way of writing a mixed number. For example, instead of 1 2/5 (a mixed number), you could write 7/5. For most algebraic manipulation you will actually want your mixed numbers written as improper fractions. When providing answers, however, mixed number format is often preferred.
To rewrite an improper fraction as a mixed number, you subtract a multiple of the denominator from the numerator and write that multiple in front of the resulting fraction.
As a simple example, let’s take 3/2.
- Subtract a multiple of the denominator from the numerator. The denominator: the denominator (bottom number) is 2, so multiples of 2 are 2, 4, 6, 8…; The biggest multiple of 2 we can subtract from the numerator is just 2 · 1 = 2.
- Write that multiple (in this case, 1) in front of the resulting fraction: 3 – 2 = 1, so we write 1 1/2.
What about 100/6? The same method works here as well. The closest multiple of six to 100 is 96, 16 times 6, so we subtract that from the denominator, write the multiple in front, and say 100/6 = 16 4/6. This can be simplified further by dividing both numerator and denominator by 2: 16 2/3.
Note the simplification could take place either before or after our improper fraction is rewritten as a mixed number. The end result would be the same.
Integers
An integer is a number than can be written on its own, without a fraction. They include the whole numbers (counting numbers 1, 2, 3, …) and their negative counterparts (-1, -2, -3, …). For example, these are all integers: {-9, 0, 1, 976}.
Non integers are everything else. In other words, if it’s not a whole number, a negative (whole) number, or zero, then it’s a non-integer.
Integer: The Building Block of Math
“God made the integers, all else is the work of man” Leopold Kronecker (7 December 1823 – 29 December 1891)
The above quote says it all, because every type of number you use in math can be made from the integers. For example:
- Decimals can be thought of as just a series of integers. For example 839.9978 is just a sequence separated by a decimal point.
- Rationals are a quotient (division) of two integers. For example, 23/49 is a ratio of 23 and 49.
Every integer is also a rational number, because you can rewrite it as that number over one: 1/1 = 1, 10/1 = 10, 98876/1 = 98876/1. If this is a little confusing (all integers are rationals and all rationals are quotients of integers), it might be helpful to remember that the integers are the building blocks: you can write one without a rational, but you can’t write a rational without an integer!
Notation
A common way to denote that a variable “x” is an integer is to use the notation I(x). The set of integers is sometimes denoted by a bold Z (from the German word Zahlen, which means “numbers”).
See also:
The Floor and Ceiling Function
References
Caldwell, C. (2019). The Prime Glossary.
Henle, J. & Kleinberg, E. (2014). Infinitesimal Calculus. Courier Corporation.
Miller, Jeff (2010-08-29). “Earliest Uses of Symbols of Number Theory”. Retrieved 2010-09-20.
References
Number, Operation, and Quantitative Reasoning. Mathematics TEKS Refinement 2006. Tarleton State University. Retrieved from https://www.tarleton.edu/ORG/team/documents/kto5/k5lessons/5/operation5_3.pdf on Feb 8, 2019.
OpenLearn: Improper Fractions. Free Learning From the Open University. Retrieved from https://www.open.edu/openlearn/ocw/mod/oucontent/view.php?id=18436§ion=4.1 on Feb 8, 2019
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 146, 1984.