The Clausen function (also called the Clausen Integral) is a transcendental, special function related to the dilogarithm of complex argument. It is widely used in experimental and higher-dimensional mathematics, and physics—especially in quantum theory. It’s usefulness stems in part because many indefinite integrals of trigonometric functions and logarithmic functions can be expressed in closed form with Clausen functions.
The Clausen function is intimately connected with various other functions including the polygamma function, Dirichlet eta function and the Riemann zeta function. The Lobachevsky function is basically the same function with a change of variable.
The function is named after Thomas Clausen, who first investigated it in 1832.
Formal Definition of the Clausen Function
The function is usually defined as the following integral (hence the alternate name of the Clausen Integral):
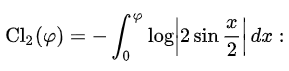
While this particular form is often called “the” Clausen function, other forms of the integral do exist. For example, Junesang (2016) formulated a new definite integral formula for by using a known relationship between the Clausen function and the generalized Zeta function.
Several other forms can be found in the literature. One of the more common is the trigonometric Clausen function, defined as (Lewin, 1981):
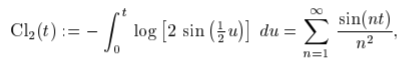
It is a periodic function, with period 2 pi.
The alternating Clausen function is defined as (Lu, 1992):
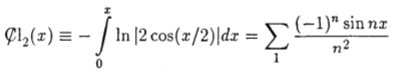
Other forms include the hyperbolic and alternating hyperbolic Clausen functions:
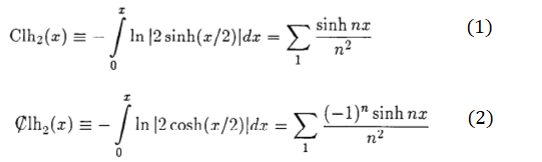
References
Abramowitz, M. and Stegun, I. A. (Eds.). “Clausen’s Integral and Related Summations” §27.8 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 1005-1006, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Junesang, C. Some integral representations of the Clausen function Cl2(x) and the Catalan constant G. East Asian Mathematical Journal. Volume 32 Issue 1 / Pages.43-46 / 2016
Lewin, L. Polylogarithms and Associated Functions, Elsevier (North-Holland), New York, London, and Amsterdam, 1981
Lu, H. Dressed Skeleton Expansion and the Coupling Scheme Ambiguity Problem. 1992.