A ramp function usually starts at the origin and travels upwards or downwards to the right in a straight line.
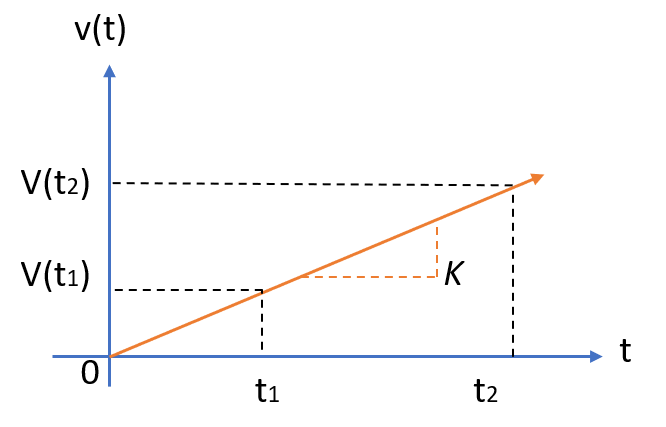
Ramp functions that don’t start at the origin (e.g. they start at x = 1, x = 5, or x = 99) are called shifted or delayed ramp functions.
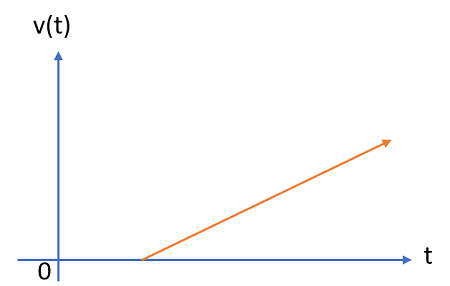
A ramp function with a constant slope (K) of 1 is called the unit ramp function. Before the origin (i.e. for negative x-values), the unit ramp function always has a value of zero.
Ramp functions are unary real functions, which take one argument and have a domain of real numbers.
Ramp Function Formula
The ramp function is defined as (Tan & Jiang, 2007):
v(t) = Ktu(t)
Where “K” is the slope, given by the following formula:
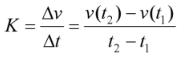
A positive slope means that the line will travel upwards; A negative valued slope will travel downwards.
These functions can also be defined as piecewise functions:
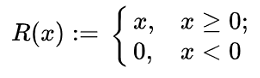
The symbol ” := ” just means “definition.” The second part of the piecewise function (0, x < 0) is just saying that the function is zero for all values less than 0. So, nothing has changed here: this is just a more formal way of defining the ramp function’s behavior.
Various other, formal ways to define the function exist, including as an integral of the Heaviside function:
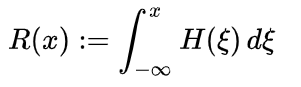
References
Tan. L. & Jiang, J. (2007). Fundamentals of Analog and Digital Signal Processing. AuthorHouse.