What is a Non Negative Function?
A non negative function has function values equal to or greater than zero (i.e., f(x) ≥ 0). The domain (inputs) of the function can be negative, but the outputs (y-values) must be zero or greater in order for the function to be classified as non-negative. A positive function is similar, except that it does not include zero in its range.
An example of a non negative function is shown on the following graph of a sine function:
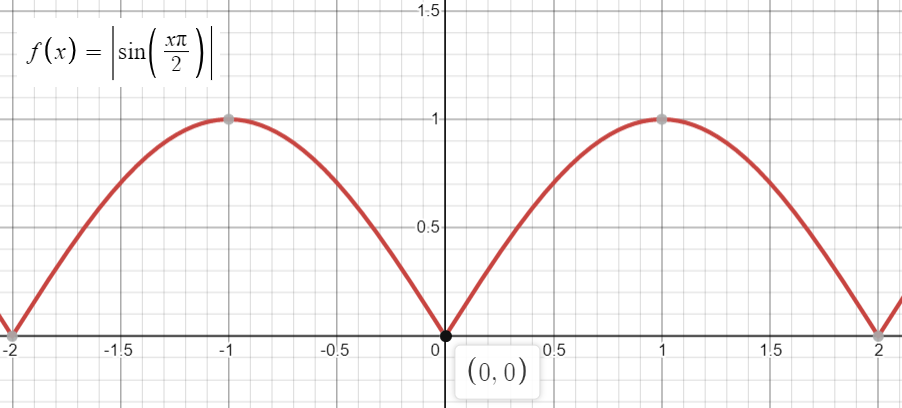
Note the labeled point [0, 0]: the function values are zero an infinite number of times and all other values are always positive.
Classifying non negative functions might seem like a pedantic exercise, but these functions play an important role in calculus, real analysis, and many other branches of mathematics. If a function is non-negative, then its integral is the area between two points a and b. If that are is equal to 1, then the integral is the probability density function.
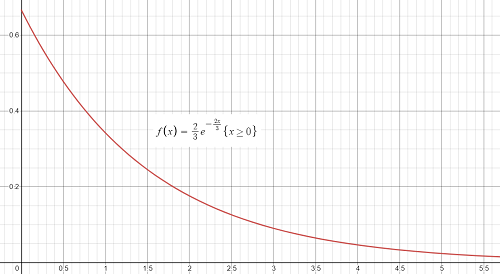
As another example, let’s say we had an integrable function on [0, ∞), its limit at infinity might not exist, but if the integrable function is non negative, and if any of the first four derivatives are bounded in a neighborhood of each relative maximum of f, then its limit does exist [1].
References
Graphs: Desmos.
[1] Dix, J. (2013). Existence of the limit at infinity for a function that is integrable on the half line. Rose-Hulman Undergraduate Mathematics Journal. Spring.