Factorial Function: Definition, Double, Generalized, Hyper-

Types of Function > Factorial Function

Contents: (Click to skip to that section):

1. What are Factorials?
   • Why 0 factorial equals 1.
2. Double Factorial
3. Factorial Function
4. Generalized Factorial Function
5. Hyperfactorial

See also:
Subfactorial: Simple Definition

What are Factorials?

Watch the video or read the article below:

When you see the ! symbol after a number, that means it’s a factorial:

• 6! is “six factorial.”
• 3! is “three factorial.”

To solve, just multiply “n” by every whole number below it. For example, if n is 3 then

3! is 3 x 2 x 1 = 6. 

It’s really just a shorthand way of writing numbers. For example, instead of writing 479001600, you could write 12! instead (which is 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1). Much easier! Here are a few more examples:

• 1! = 1
• 2! = 2
• 3! = 6
• 4! = 24
• 5! = 120

The formal definition: Factorials are products of every whole number (counting numbers
1, 2, 3…) from 1 to n.

Factorials are used in many areas of statistics, including the factorial distribution.

Why does zero factorial equal 1?

If you’re wondering why zero factorial equals 1, you’re not alone. It’s one of the great puzzles of mathematics that seems completely unintuitive. There are a few different ways to show that 0! = 1 must be true:

1. With the Definition,
2. With the combinations formula (from statistics),
3. With limits (calculus).

The Definition

The reason why 0! = 1 is because it’s defined that way.

“…zero factorial equals 1, 0! = 1 [and] 1! = 1. However, one cannot similarly conclude that 0 = 1 because the one result is arrived at by convention and the other result is a mathematical fact. As with all conventions certain protocols and rules must be followed in arithmetic operations involving zero” [1].

If you’re having trouble wrapping your head around that statement, you’re not alone. For millennia, mathematicians debated about whether or not zero (even without the factorial) existed at all! [2] The Roman Numeral system didn’t have zeros, and it wasn’t until the introduction of the decimal system in the 13th century that “zero” really became a thing. Still, working with “0” results in a lot of problems, including the unintuitive idea that 0! = 1.

Showing 0! = 1 with the Combinations Formula

Note: You may want to read “What is a Factorial?” first.

We want to show that there’s only one way of choosing zero items (that zero factorial equals one) with the combinations formula from statistics:

• _nC_r = n! / ((n – r)! r!)

Where:

• n = Number of items.
• r = How many items are taken at a time.

Let’s start with three items and move backwards, so see if there’s a logical pattern.

Let’s say you had three novels on a shelf and you wanted to choose three at the same time. How many different ways could you grab all three at once? Logically, you’d say there’s only one way of grabbing all three. But you can show this with the combinations formula. We have n = 3 and r = 3, so:

₃C₃ = 3! / ((3 – 3)! 3!) = 1.

This is the answer we would expect. Now let’s try two books:

₃C₃ = 2! / (2 – 2)! 2! = 1.

Are you seeing the pattern? As long as you’re taking all of the items at the same time (we don’t care what order they are in), it’s always going to equal 1. You could put in 99,999 or 1 million and you would still get: 1.

Now we’ve established the logic, take a close look at one example:

• = 2! / (2 – 2)! 2!
• = 2 / (0)!*2

We know that this equation must equal two. The only way to make that happen is if 0! = 1. Otherwise you would have division by zero, which is not defined.

What happens if we follow our initial intuition and decide that 0! = 0? That would that the number of ways of choosing 3 books from a set of three would be undefined:

• = 3! / (3 – 3)! 3!
• = 6 / (0)*3 = undefined.

Show that Zero Factorial Equals One With Limits

The following explanation [3] is fairly easy to follow with some basic calculus concepts.

1. Let’s define a factorial for items equal to or greater than one (we’re going to ignore 0! for a moment).
   Definition: The factorial n is defined by n! = (n)(n – 1)…(3) (2) (1) for all n ≥ 1.
2. The lower bound for [1] must be 1, because 1ⁿ = (1) (1) (1) … → 1 ≤ n.
3. We can define an upper bound in the same way: n! ≤ (n) (n) (n) … = nⁿ.
4. Putting (2) and (3) together, we get: 1 ≤ n! ≤ nⁿ.
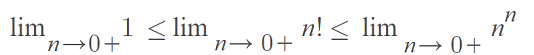
5. The upper bound in (4) is valid for n > 0, so take the limit as n → 0⁺: This limit is indeterminate because 0ⁿ = 0 for any n > 0 and n⁰ = 1 for any n ≠ 0.
6. From (5), we can say that
   
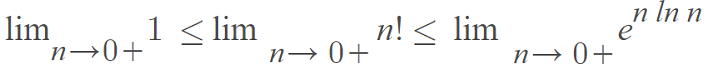
7. Using L’Hospital’s rule, we have the limit of n ln n (as n→ 0⁺)

= 0. We can deduce that:


8. If we let the limit n! in (7) equal zero, we get: 1 ≤ 0! ≤ 1, which implies that 0! = 1.

References

[1] Zero in Four Dimensions: Cultural, Historical, Mathematical, and Psychological Perspectives.
[2] Seife, C. (2000). Zero: The Biography of a Dangerous Idea. Penguin Books.
[3] Mahmood, M. & Mahmood, I. (2015). A simple demonstration of zero factorial equals one. International Journal of Mathematical Education 47(6):1-2

Double Factorial

A double factorial (n!!) is a product of all integers from 1 to n that have the same parity (i.e. they are either odd or even) as n; In other words, it’s the product of every other integer less than or equal to n. For example:

• 7!! = 7 * 5 * 3 * 1,
• 8!! = 8 * 6 * 4 * 2 * 1,
• 9!! = 9 * 7 * 5 * 3 * 1,

Use in Calculus

Factorials are used fairly infrequently in calculus (they are more common in precalculus), but they do pop up now and again, especially when you’re working with sequences and series. For example, the ratio test is very useful when you’re working with series containing factorials.

Factorials and Calculators

Most calculators have a button for this; It’s usually hidden in a menu somewhere. On the TI 83, you can find it in the “PRB” menu. If you’re on the internet (which you probably are if you’re reading this), Google can also do the work for you. Just use a regular exclamation mark (!).

• Go to the search bar at Google.com
• Type in a factorial, such as 12!
• Press enter
• 12 ! = 479 001 600

Google can also figure out more complicated factorials for you, like 36! / (12-10)!6!. Make sure you put in parentheses and a multiplication sign (just as you would on any basic calculator). Like this:
36! / ((12-10)! * 6!) = 2.58328699 × 10³⁸

Google Calculator Tip: To multiply using Google, use an asterisk (*) instead of a “×” symbol.
The factorial function is defined for all positive integers (1, 2, 3…) as

y = F[n] = n!

Formal Definition of Factorial Function

The recursive definition of the factorial function (n!) is defined for natural numbers (whole, non-negative numbers that we use to count) n as follows:
n! = n(n – 1)(n – 2)…3 · 2 · 1

It’s called “recursive” because the same multiplication is performed over and over again, with each input multiplied by the previous result.

Example: Use the recursive definition of the factorial function to find 3!.
Solution: 3! = 3 x 2! = 3 x 2 x 1! = 3 x 2 x 1 x 0! = 3 x 2 x 1 x 1.

A Generalized Factorial Function

The factorial function doesn’t make sense when x = 0, so a workaround was the development of the more generalized gamma function:

gamma (n + 1) = n!

The gamma function handles zero, as well as all real-valued positive values and complex numbers.

You’ll find the factorial function used in many areas of calculus, including Faà di Bruno’s Formula, the Beta Function and lambda calculus. They also appear in Taylor’s theorem, which finds the error for a function expressed as a power series; This appearance is in part because the nth derivative of xⁿ is n! (Beaumadier & Hausenblas, n.d.).

The function can be also be extended to all real numbers with the following definite integral (Edwards, 1974):

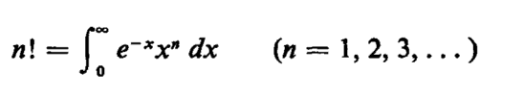
Hyperfactorial

The hyperfactorial function multiplies a sequence of consecutive integers from 1 to a specified number, with each integer raised to its own power. It is an extension of the basic factorial function.

Examples

It’s relatively easy to calculate a small hyperfactorial by hand. Just:

1. Write out all the integers from 1 through the number given,
2. Raise each integer to its own power,
3. Multiply through.

For example, 3 hyperfactorial, written as H(3), is calculated as follows:

1. Write out all the integers from 1 through the number given: 1, 2, 3,
2. Raise each integer to its own power: 1¹, 2², 33
3. Multiply through: 1¹ * 2² * 33 = 1 * 4 * 27 = 108
   .

The first 11 hyperfactorials (i.e. for integers 1 through 11) are (OEIS A002109):

1. 1
2. 1
3. 4
4. 108
5. 27648,
6. 86400000,
7. 4031078400000,
8. 3319766398771200000,
9. 55696437941726556979200000,
10. 21577941222941856209168026828800000,
11. 215779412229418562091680268288000000000000000,
12. 61564384586635053951550731889313964883968000000000000000

As you can see, the hyperfactorial grows rapidly (although not as rapidly as the superfactorial). So rapidly in fact that H(14) is almost equal to a googol.

Extension of the Hyperfactorial

Although it’s usual to use integers, the definition can be extended. For example, Ciucu & Krattenthaler (2013) extend the definition to half-integers (i.e. odd integers divided by 2) in their paper on plane partitions, from: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=1FE18601EF778E99BA70C7AE8D35D5B2?doi=10.1.1.406.4522&rep=rep1&type=pdf

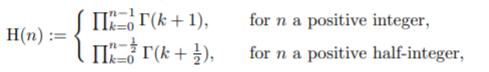
The K Function

The “K function” is a generalization of the hyperfactorial to complex numbers.

Note that the term “K function” is widely used in mathematics for widely different functions. For example, Ripley’s K-function has a very different meaning from the k-function related to hyperfactorials.

References

Beaumadier, J. & Hausenblas, M. (n.d.). Factorial n!. Retrieved July 10, 2020 from: http://factorielle.free.fr/index_en.html
Benjamin, A. & Brown, E. (2009). Biscuits of Number Theory. Mathematical Association of America.
Ciucu, M. and Krattenthaler, C. A Dual of Macmahon’s Theorem on Plane Partitions. Proc. Natl. Acad. Sci. USA, vol. 110 (2013), 4518-4523)
Dr. Math. x Factorial and the Gamma Function. Retrieved July 10, 2020 from: http://mathforum.org/library/drmath/view/54540.html
Edwards, H. (1974). Riemann’s Zeta Function. Elsevier Science.Fletcher, A.; Miller, J. C. P.; Rosenhead, L.; and Comrie, L. J. An Index of Mathematical Tables, Vol. 1, 2nd ed. Reading, MA: Addison-Wesley, p. 50, 1962.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 477, 1994.
Sloane, N. & Plouffe, S. The Encyclopedia of Integer Sequences 1st Edition. Academic Press, 1995.