Contents:
What are Singularity Functions?
Singularity functions (also called singular functions) are any functions that contain singularities. The singularities can be poles, removable singularities, or essential singularities.
Singularity functions can also be defined in terms of derivatives. These functions are either not finite everywhere, or they have one or more derivatives that are not finite everywhere. In other words, one or more derivatives is discontinuous.
The opposite of a singularity function is an analytic function, where all orders of derivatives (i.e. 1st, 2nd, 3rd…) exist.
Examples of Singularity Functions
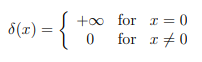

The unit ramp function and unit step function are also, popular, especially in signal processing. The unit doublet singularity function is also sometimes used; It is the derivative of Dirac’s delta function (Priemer, 1991).
Conditional Constraints
Every singularity function has a defined constraint. For example, the Heaviside step function evaluates to 0 for all values of x < a; All other values evaluate to 1. Dirac’s delta function evaluates to ∞ if x = a and 0 for every other x-value. The “a” here is a user-defined place where the function acts or starts to act.
Irregular Singularity
An irregular singularity (sometimes called singularity of the second kind or irregular single points) happens when regular (elementary) singularities (aka regular single points) in a differential equation merge, creating an ill-behaved singularity.
When the regular singularities merge, they are replaced by the irregular singularity. This creates problems with analysis because the Frobenius method (where you create a power series solution to a differential equation) usually fails for functions with an irregular singularity.
For example, the confluent Heun equation is obtained when two singularities are merged at z = a and z = ∞. The result is an equation with regular singularities at z = 0 and z = 1 and an irregular singularity at z = ∞. This cannot be solved via the Frobenius method.
Rank and Species of an Irregular Singularity
A singularity can be measured by Poincaré rank (defined as h := g + 1), which are how far away the singularity is from being “regular” (regular singularities have a rank of 0). So, an irregular singularity of rank 1 would be better behaved than one of rank 2. Other ways to measure severity do exist, including Ince’s rank (1926), which is equivalent to twice the “regular” rank. Another measure, species, is defined as “…two less than the number of of elementary singularities needed to produce it by confluence” (Ronveaux, 1995)
Examples of a Function with an Irregular Singularity
Airy’s equation y′′ – xy(x) = 0 has an irregular singularity at x = ∞. As x tends to larger and larger values, the leading behavior is (Evans, n.d.):
![]()
Removable Singularity
A removable singularity in complex analysis is similar to a removable discontinuity in real analysis. “Removable” means that you can “fill in” the hole in a discontinuous function, making it continuous.
Removable singularities are one of three types of singularity. The other two are isolated singularities (poles) and essential singularities.
What Makes a Singularity “Removable”?
A “singularity” is a point where a complex-valued function isn’t analytic. A removable singularity is a point where the function is undefined. It can be removed by assigning the undefined spot a value representing the limit as you approach that point.
Example of a Removable Singularity
As an example, the sinc function f(z) = sinc(z)/z is undefined at z (because of division by zero). However, you can take the limit as the function approaches zero and replace the function value at 0 with the value for the limit. For this function, the limit is 1 at z = 0, so you can remove the singularity with sinc(0) = 1.
Alternate Definition of Removable Singularity
Another way to define removable singularities is by taking the derivative. A function f has a removable singularity at point a, if f can be defined at a in a way that makes the new function differentiable at a. This is really saying the same thing: If you remove the singularity by assigning a limiting value, then that function will become continuous (and therefore differentiable).
References
Arfken, G. “Singular Points.” §8.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 451-453 and 461-463, 1985.
Buckmore, R. (2014). Complex Analysis.
Evans, M. Section 8: Power Series Solutions of ODEs. Retrieved December 26, 2019 from: https://www2.ph.ed.ac.uk/~mevans/amm/lecture08.pdf
Ince, E. (1926). Ordinary Differential Equations. Dover.
Knopp, K. “Singularities.” Section IV in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 117-139, 1996.
Krantz, S. G. “Removable Singularities, Poles, and Essential Singularities.” §4.1.4 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 42, 1999.
Norton,R. (2013). Machine Design (5th Edition). Pearson.
Priemer, R. (1990). Introductory Signal Processing (Advanced Electrical and Computer Engineering) (v. 6). World Scientific Publishing Company.
Image: Functor Salad [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0/)]
Ronveaux, A. (1995). Heun’s Differential Equations (Oxford Science Publications) 1st Edition. Clarendon Press.
Pushpin image: Clipart-Library.