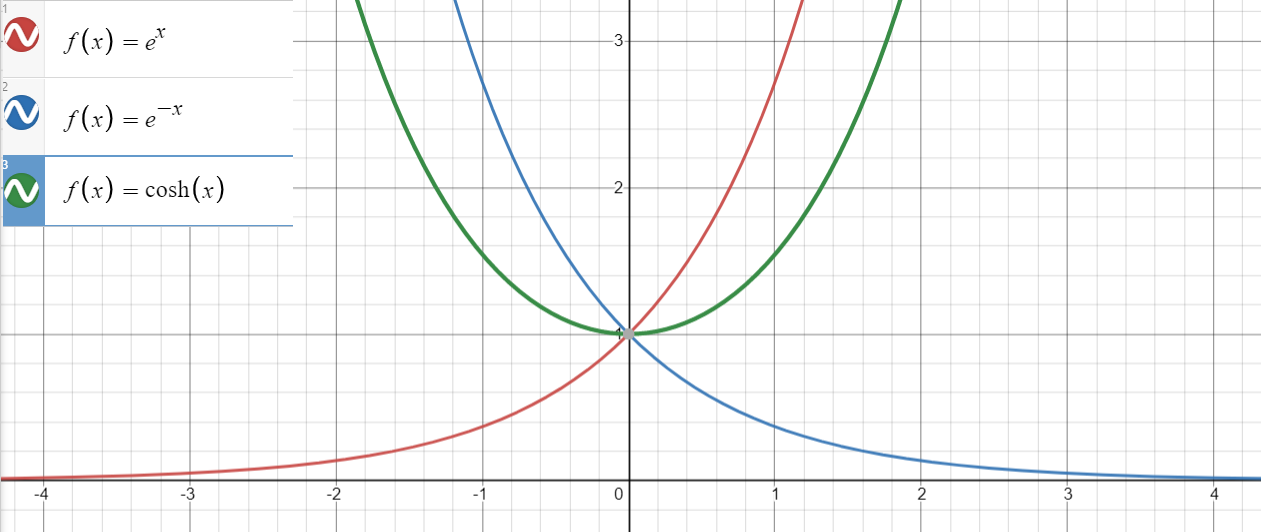
The hyperbolic cosine function, denoted coshx and pronounced like it rhymes with “gosh”, is the average of the exponential functions ex and e-x, where e is Euler’s number.:
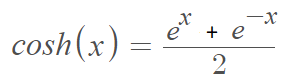
For the traditional cosine function with a complex argument, the identity is
cosh(x) = cos ix.
The derivative of cosh(x) is sinh(x), where sinh(x) is the hyperbolic sine function.
Properties of Hyperbolic Cosine Functions
Cosh(x) is an even function (i.e., cosh(-x) = cosh x), which means it is symmetric about the y-axis.
The hyperbolic cosine function has a domain of (-∞, ∞) and a range of [1, ∞). It is not a one-to-one function; it fails to pass the horizontal line test, which means that the function is not invertible unless an appropriate domain restriction (like x ≥ 0) is applied. As the function is increasing on the interval [0, ∞), it has an inverse function for this domain.
The hyperbolic cosine and hyperbolic sine functions share some important properties [1]:
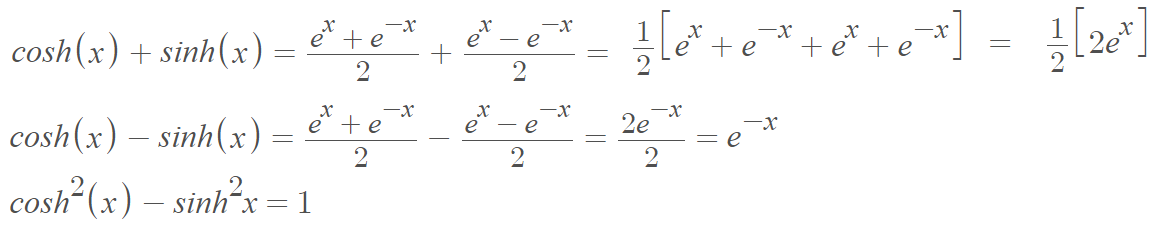
History and Uses of the Hyperbolic Cosine Function
The hyperbolic cosine function calculates the hyperbolic cosine of an angle. It is an example of a hyperbolic trigonometric function which has measures based on the hyperbola instead of the unit circle which is the basis for the “usual” trigonometric functions. This has been around since the 1700s when it appeared in works by many prominent mathematicians like Jacopo Riccati (1759) and Johann Lambert (1768). It is used as a measure of distance in some types of non-Euclidean geometry and has many real life applications, especially in engineering. For example, it can describe the curve formed by a high-voltage power line suspended between two towers [2]. Architects Eero Saarinen and Hannskari Bandal used the hyperbolic cosine function to design the Gateway Arch in St. Louis [3].
References
[1] May, J. Section 4.5 Hyperbolic Functions. Retrieved December 19, 2021 from: https://www.math.uh.edu/~jen/winter%20mini/Notes/filled%20in%20notes/1431S45fi.pdf
[2] Encyclopedia Brittanica. Catenary.
[3] Hyperbolic Functions. Retrieved December 23, 2021 from: http://www.math.udel.edu/~angell/hyper.pdf