Parabola: Definition, Examples, Find Vertex

Calculus Definitions >

Contents:

1. What is a Parabola?
   • Directrix and Focus
   • Equations for the Parabola
2. What is a Vertex?
   • Finding the Vertex

What is a Parabola?

A parabola is a U-shaped line or curve. It’s the graph of a quadratic function.

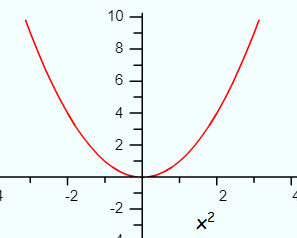
Parts of a Parabola

A parabola is made up of a set of points that are equidistant from:

1. The directrix: a fixed line, and
2. The focus: a fixed point.

The illustration below shows how the directrix and focus are related in distance (note that the lengths of the two pink line segments are the same):

Any point on a parabola will be at an equal distance from both the focus and the directrix.  Parabolas can either open up (concave up) or down (concave down).  They will always have one y-intercept and may or may not have x-intercepts. 

Other parts shown in in the image:

• Vertex: The highest or lowest point of a parabola (the point at which the parabola makes the sharpest turn).  It is halfway between the focus and directrix. 
• Latus rectum: a line segment that runs through the focus. It is perpendicular to the axis of symmetry and both of its endpoints are located on the graphed curve. 

Equations for the Parabola

The standard equation for a vertical parabola (like the one in the chart above) is:

y = x²

For a horizontal parabola (an opening facing the left or right) the formula is:

y² = x

To find the focus of a parabola, use the following formula:

y² = 4ax

Example:

Find the focus of the equation y² = 5x

First convert y² = 5x into y² = 4ax form.

y² = 4(5/4)x

The value of a = 5/4.  So the focus of y² = 5x is:

F = (a,0) = (5/4,0)

What are Parabolas used for in Real Life?

An example of a parabola you encounter in your everyday life is a satellite dish.  Satellite dishes are useful because they have a certain useful property of parabolas in general.  Any ray (in the case of a satellite a signal) parallel to the axis of symmetry will be reflected off of the surface of the dish and be routed directly to the focus.  In this way, satellite dishes are able to transmit and receive signals.

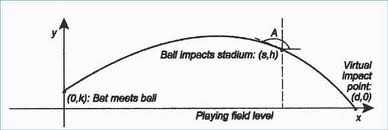The path of a hit baseball also follows this kind of shape. A baseball’s graph can be represented in calculus using a pair of parametric equations with time as the dimension. See: Path of a Baseball.

What is a Vertex?

A vertex is a high or low point on a curve. In calculus, they are usually called minimums or maximums.

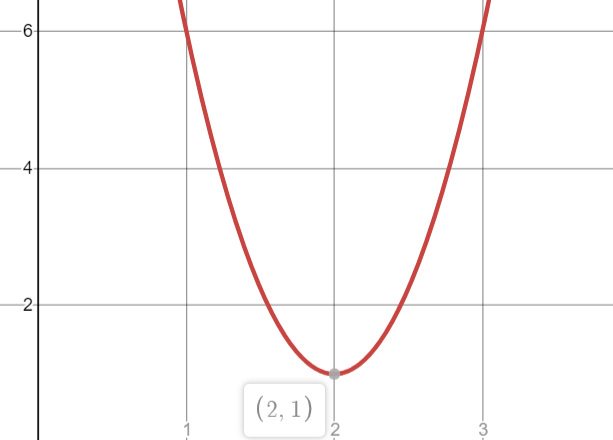
Finding the Vertex

There are a few ways to find a vertex, including completing the square in algebra. In calculus, the main way to find a vertex is by finding the derivative (a.k.a. slope). At any vertex, the derivative will be equal to zero, so a little algebra will find the vertex’s location.

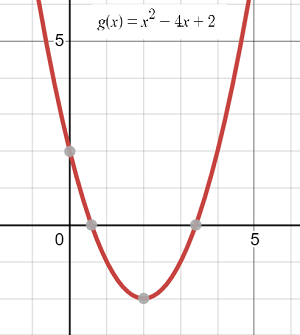
Example problem: What is the vertex of the function g(x) = x² – 4x + 2?

Step 1: (Optional) Graph your function. This will enable you to see if you’re looking for one or more vertices and whether they will be minimums or maximums. I used Desmos.com to graph this particular function. The graph shows the function has one vertex, and it’s a global minimum.

Step 2: Find the derivative. For this function, we can use the power rule (as well as the sum rule):
g′(x) = x² – 4x + 2 = 2x – 4.
If you aren’t very familiar with the power rule, watch this short video for a few examples:

Step 3: Set your derivative equal to zero:
2x – 4 = 0

Step 4: Solve the equation from Step 3 to find the vertex’s x-value:

• 2x – 4 = 0 →
• 2x = 4 →
• x = 2

Step 5: Place the value you got in step 4 into the original function. Solve to find the vertex’s y-value:
g(x) = x² – 4x + 2 →
= 2² – 4(2) + 2 →
= 4 – 8 + 2 = -2

The vertex is at (2, -2), which is exactly what we expected when we created the graph in Step 1. You may see at this point why creating the graph is a good idea: it gives you a way to double check your solution.

References

Anton, H, Calculus: A New Horizon, Vol. 2 (6th Edition). Wiley.
Griewank, A. & Walther, A. (2008). Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. Society for Industrial and Applied Mathematics.
Kac, V. Vertex Algebras for Beginners. American Mathematical Society. 1997.
Kuttler, K. (2010). Calculus: Theory and Applications, Volume 1. World Scientific.

Related articles

Polynomials: A second degree polynomial has a U shape.
Vertical line test: answers the question Are parabolas functions?