Contents (Click to skip to that section):
1. Secant Line Definition
A secant line (from the Latin Secare, to cut) connects two ore more points on a curve.
The following image shows a secant line that connects two points, along with a tangent line (which skims the curve at one point):
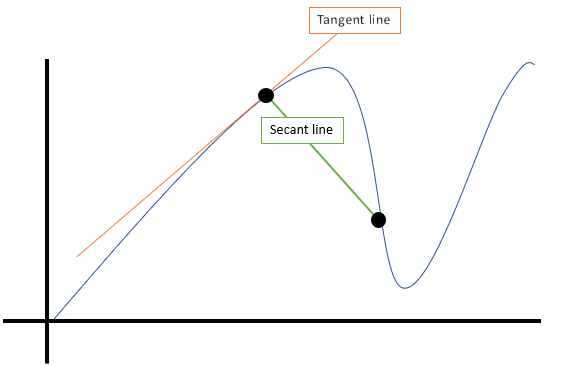
A secant line is useful to calculate the slope of a line. A secant line is the equivalent of the average rate of change or the slope between two points. Once you have calculated the slope of a line we can find the equation of the line through the two points. The two points of a secant line are denoted by:
(x1, y1) and (x2, y2)
Slope of a Secant Line
The slope of the secant line is calculated using the formula:
(y2 – y1) / (x2 – x1)
The equation of the line through the two points can be found by using the slope-point formula:
y – y1 = m(x – x1)
Finding the Equation of a Secant Line
Finding the equation of a secant line is a three-step process:
- Locate two points on the secant line.
- Find the slope of the line that runs between the two points.
- Find the equation using the point slope formula.
Example:
Question: Find the equation of the secant line to the curve
f(x) = 4x2 – 7 where x = -2 and x = 1.
Step 1: Find Two Points:
The question gives us the values for x so we must determine the y values in order to calculate the slope of the line. We will calculate for x = -2 first:
- f(-2) = 4(-2)2 – 7
- = 4(4) – 7
- = 9
So the coordinates of the first point are (-2, 9). Next, find the coordinates of the second point x = 1.
- f(1) = 4(1)2 – 7
- = 4 – 7
- = -3
The coordinates for the second
point are (1, -3).
Step 2: Find The Slope:
Now that we have the coordinates for the two points we can find the slope of the line.
- m = 9 – (-3) / -2 -1 = 12/-3 = -4
The slope of the line between the two points is -4.
Step 3: Find The Equation:
Plug the slope into the slope-line formula to find the equation of the line.
- y – y1 = m(x – x1) = y – (-3) = -4(x – 1) = y + 3 = -4x + 4
- y = -4x + 1
The equation is y = -4x + 1.
Secant Function
Contents (Click to skip to that section):
- What is the Secant Function?
- Limit of a Secant Function
- SEC function in Excel
The secant function (also called the sec function) is the reciprocal function of the cosine function. It is defined as:
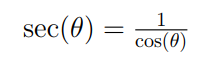
The domain for the secant function is all values for which cos ≠ 0. In other words, for all odd half integer multiples of π. At these points, the function has vertical asymptotes. The period for this function is 2π.
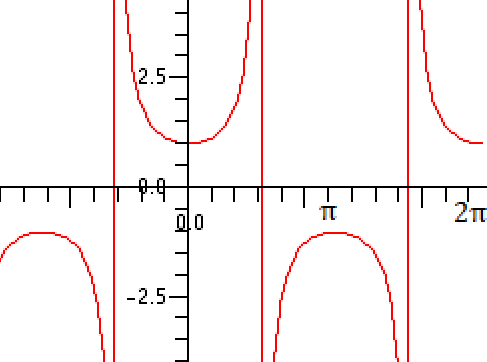
Limit of a Secant Function
Finding the limit of a secant function can seem imposing when you look at a graph of the function, but approaching the limit in small steps (by making a table) makes it relatively simple. One key fact to keep in mind is that if a limit does not approach the same value from the left and the right, then the limit does not exist.
Example Problem: Find the limit of sec (x) as x approaches 1.
Step 1: Draw a table . Include a few small values around your x-value. In this table, I’m finding the limit at the point c = 1.00 (in the center of the table).
| x | 0.70 | 0.90 | 0.99 | c = 1.00 | 1.01 | 1.10 | 1.30 |
| f(x) |
Step 2: Evaluate for the value of the function at the x values you set up, using a calculator. I used Google for these calculations (for example, type in “secant(0.70 degrees)”). If you get don’t get the answers I did below, make sure your calculator is using degrees, and not radians.
| x | 0.70 | 0.90 | 0.99 | c = 1.00 | 1.01 | 1.10 | 1.30 |
| f(x) | 1.00007 | 1.00012 | 1.00015 | 1.00015 | 1.00016 | 1.00018 | 1.0026 |
Step 3: Analyze the calculated values to find the limit. If the limit isn’t clear, but the values do seem to be heading towards a limit from both sides, continue to use numbers closer and closer to c to narrow down the limit.
In this example, the values are trending towards 1.00015.
Example Problem: Find the limit of sec (x) as x approaches 90.
Step 1: Repeat the above steps for the new values.
| x | 89.70 | 89.70 | 89.99 | c = 0.90 | 90.01 | 90.10 | 90.30 |
| f(x) | 190.99 | 572.96 | 5729.5 | Undefined | -5729.5 | -572.96 | -190.99 |
The function is undefined at 90, and approaching 90 from the left tends towards infinity, while approaching 90 from the right tends towards negative infinity. In this case, the limit of a secant does not exist. For the secant function, this will occur at 90 and at every interval of 180 either direction from it.
SEC Function in Excel
The SEC function in Excel gives you the secant of a certain angle. The format is:
SEC(number)
Where “number” is the angle (in radians) for which you want the secant.
Note: If your angle is in degrees, Google will convert it for you.
For example, =SEC(45) gives you the secant of a 45 degree angle, which is 1.90359.
Exsecant Function
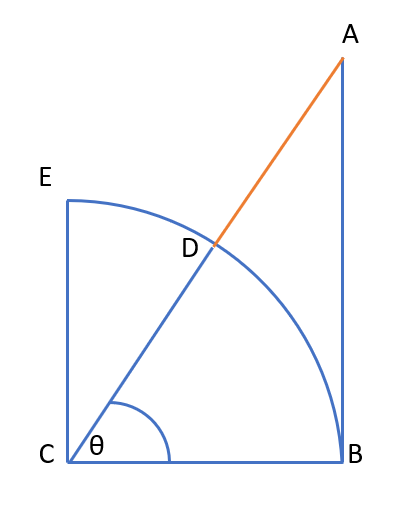
The exsecant function is an archaic function defined as:
exsec(x) = sec(x) – 1 = tan(x) · tan(½ x)
or, defined in terms of an angle (θ):
exsec θ = sec θ – 1
The word is a contraction of external secant.
Meaning of the Exsecant Function
The exsecant function gives you the part of the secant line that’s outside the unit circle, which is a circle with a radius of 1. The segment inside the circle is 1, so all you have to do to find the exsecant is to:
- Find the secant of the angle (length AC in the above image),
- Subtract 1.
An Archaic Function
The function was once an important part of surveying, astronomy and sea travel, appearing in many nautical and astronomical tables. It is now used infrequently, because tables have fallen out of everyday use and you can calculate the exsecant directly.
References
Chapter 8 Families of Functions. Retrieved December 19, 2019 from: http://www.ms.uky.edu/~droyster/courses/fall06/PDFs/Chapter08.pdf
Trigonometry. Retrieved December 19, 2019 from: https://mysite.du.edu/~jcalvert/math/trig.htm
Oldham, K. et al. (2010). An Atlas of Functions: with Equator, the Atlas Function Calculator. Springer Science & Business Media.
Office Support: SEC Function. Retrieved May 28, 2019 from: https://support.office.com/en-ie/article/sec-function-ff224717-9c87-4170-9b58-d069ced6d5f7
Schwatzman, S. (1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. MAA.