A general “trinomial” has three terms, usually in the form ax2 + bx + c. When that trinomial also meets the requirements for being a function (e.g. each input matches to one output), it’s called a trinomial function.
Differing Definition
Be careful when interpreting the term “trinomial function”. You won’t find the term clearly defined in mathematics textbooks. There doesn’t seem to be an agreed upon exact definition, so you may read about a function defined slightly different from above. As an example, this article on the subject of partial derivatives defines it as:
“A trinomial function in terms of three variables: x, y, and z. In each term of the trinomial, the variables are taken to integer powers between 0 and 5 (inclusive), and they may be multiplied by each other.”
There’s no mention in that definition of a standard form, or the highest degree being “2”. It’s simply any expression with three terms.
Historically, trinomials were also defined loosely. Dana & Dana (1889) defined one particular trinomial function of having the form n′ = α + Βn + yn2 (this is really just the same thing except it isn’t in the standard form of highest power first). Another example of a slightly different definition: De Morgan (1837) defined it as an “Integral function…containing three distinct powers.”
Graph of a Trinomial Function
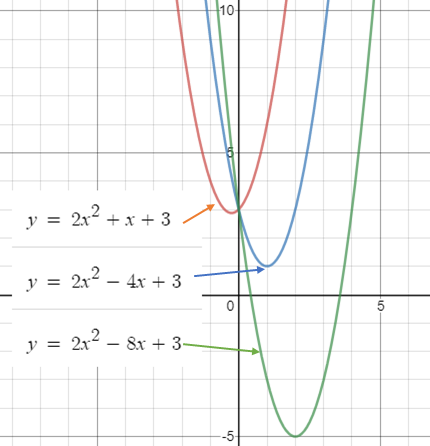
A trinomial function can have vastly different looking graphs, depending on which terms are included in the definition. A general trinomial of the form ax2 + bx + c has a graph in the shape of a parabola:
References
Dana & Dana (1889). The American Journal of Science.
De Morgan, A. (1837). The Elements of Algebra preliminary to the Differential Calculus, and fit for the higher classes of schools, etc. Taylor and Walton.
Talbot, R. (2004). Polynomials. Retrieved December 18, 2019 from: http://faculty.smcm.edu/dtkung/seeing_connections_abstract_algebra_HS_math/3polynomials/3c_poly.html