Contents:
What is an Interval of Convergence?
The interval of convergence is a set of x-values on which a power series converges. In other words, it’s the interval of x-values that you can plug in to make a convergent series. It’s possible for this interval to include all of the values in a series, a limited range of x-values, or just a single x-value at the center.
Within this interval, the series has both absolute convergence and uniform convergence.
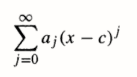
Radius of Convergence
For real-valued functions, the radius of convergence is half the length of the interval of convergence. For example, let’s say you had the interval (b, c). The radius of convergence will be R = (c – b) / 2. Two extremes are possible:
- The radius of convergence can be zero, which will result in an interval of convergence with a single point, a (the interval of convergence is never empty).
- Or, for power series which is convergent for all x-values, the radius of convergence is +∞.
The anchor point a is always the center of the interval of convergence. For real numbers of x, the interval is a line segment; for complex numbers, the interval will be a circle. If the radius of convergence is R, then the interval of convergence includes the open interval:
(a – R, a + R).
For example, if the radius of convergence is 1/N, then the interval of convergence includes (a – 1/N, a + 1/N); In order to find the interval of convergence, find the radius of convergence first then insert the result into (a – R, a + R).
For the radius of convergence for complex-valued functions, see: Circle of Convergence
How to Find the Radius & Interval of Convergence
Watch the video for an example of how to find the radius of convergence finding the root test:
The ratio test or the root test can be used. This first example uses the root test, which works by taking the limit of a series an:
![]()
Example question: What is the interval of convergence for the series:
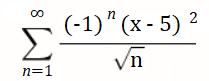
Solution (perform the root test):
Step 1: Plug the series into the formula for the root test:
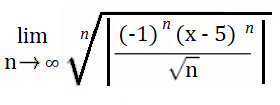
Step 2: Set the limit as an equality less than 1 (for convergence):
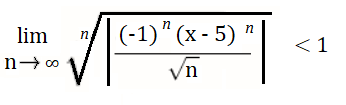
Step 3: Solve for x:
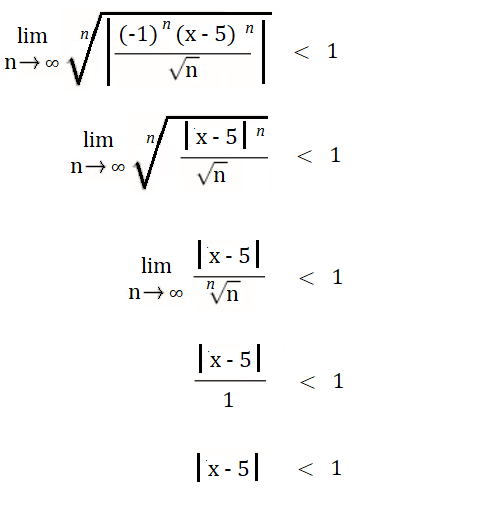
The Radius of Convergence is 1 (from the right side of the inequality).
Step 4: Plug your Step 3 answer for R into the interval of convergence formula:
(a – R, a + R) = (5 – 1, 5 + 1) = (4, 6).
*For a power series, the center is defined in the terms. Look for part of a general term in the series that looks like x – a. The center is “a“.
Ratio Test General Steps
The formula for the test is:
![]()
The basic steps for using the ratio test to find the radius of convergence:
Step 1: Form a ratio of an + 1/an, then simplify.
Step 2: Take the absolute value of the ratio and the limit as n → ∞
Step 3: Use the table below to find R.
| Result from Step 2: | R | |
| Zero | Infinite (i.e. convergence for all x-values) | |
| N · |x – a| (N is a finite, positive number) | R = 1/N | |
| Infinity | Zero (i.e. convergence at only x = a) |
A Note About Endpoints
The steps above show you how to find the interval of convergence, but they don’t tell you if the endpoints of the series are inside that interval. To find that out, plug the endpoints into the power series one at a time. Then use a convergence test to figure out if the infinite series you just created (by plugging in one of the endpoints) converges:
- If it does converge, then the endpoints are in the interval of convergence.
- If it doesn’t converge, the endpoints are not in the interval.
Don’t use the ratio test or the root test for testing the endpoints: it tends to not work well, and will likely give you inconclusive results.
Circle of Convergence
For complex-valued functions, the circle of convergence (also called the region of convergence) is the set of values for which a power series is valid [1]. The circle of convergence is basically the radius of convergence extended to the complex setting.
Formally, the circle of convergence CR(z0 is where the power series
![]()
converges at each point inside the circle.
If a function has a power series expansion around a point, then the circle will extend outward to the closest point where the function isn’t analytic; In other words, a function is analytic, but then fails to be analytic for at least one point (or perhaps all points) on the circle of convergence. This circle could therefore represent all complex numbers (ℂ), but also could represent a specific region (the complex analysis equivalent of an interval in real analysis).
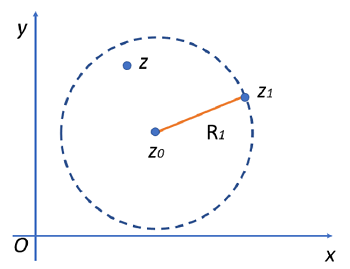
The above image shows the greatest circle centered at z0.
The radius of the circle of convergence could be infinite [2], which doesn’t work well on paper! If you’re having trouble in imagining an infinitely wide circle, think of how an arrow on the x-axis or y-axis of a Cartesian plane could also imply infinity.
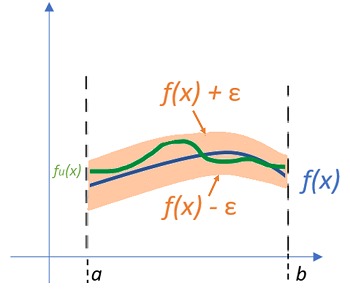
If the infinite complex power series an(z – z0)n has circle of convergence |z – z0| = R, then for any positive valued r, the series is uniformly convergent on the closed disc |z – z0| ≤ r. In addition, it is absolutely convergent for each point in |z – z0| ≤ r [3].
Interval of Convergence: References
[1] Manogue, C. & Dray, C. 7.6 Convergence of Power Series. Retrieved April 24, 2021 from: https://books.physics.oregonstate.edu/LinAlg/convergence.html
[2] Section 5.63. Absolute and Uniform Convergence of Power Series. Retrieved April 24, 2021 from: https://faculty.etsu.edu/gardnerr/5337/notes/Chapter5-63.pdf
[3] Uniqueness of Taylor Series. Retrieved April 24, 2021 from: http://web.math.ucsb.edu/~helena/teaching/math122b/taylor_series.pdf
Other references:
Belding, D. & Mitchell, K. (2008). Foundations of Analysis. Courier Corporation.
Krantz, S. (2004). A Handbook of Real Variables: With Applications to Differential Equations and Fourier Analysis. Springer Science and Business Media.
Winter, D. (2008). Recitation Handout 17: Radius and Interval of Convergence. Retrieved February 2, 2020 from: http://www.math.cmu.edu/~amanita/math122/handouts/m122_f08_rhandout17.pdf