Contents:
What is a Power Function?
A power function has the form
![]()
where:
- a and p are constants,
- p is a real number,
- and a is nonzero.
We call a the scaling factor, and p is the exponent or the power. The polynomial functions we work with in much of algebra are simply combinations of power functions.
Sometimes power functions are more narrowly defined, as
![]()
Under this definition, all power functions would pass through the point (1,1). The power functions in our wider definition are all multiples of these more narrowly defined ones.
Examples of Power Functions
The simplest power function is the one with a = 1 and p = 1; y = x.
But that is only one of many. y = x-1, y = x1/2, and y = x 6 are also power functions.
The graphs below are all graphs of power functions.
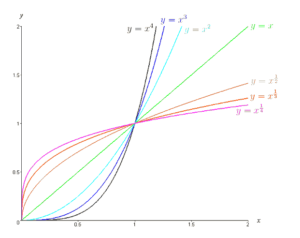
The exponent p does not have to be positive; The following are all power functions:
- y = x -1,
- y = x-1/2,
- y = x-5
Under the wider definition, y = 2, y= 4x, and y = 5x1/2 are also all examples of power functions.
The Shape of Power Functions
Suppose, for simplicity, the scaling factor a is one. Then:
- p > 1 Means the function is concave up, and grows as x grows large
- p = 1 Means the function is a straight line (y = x)
- 0< p< 1 Means the function is concave down, and grows as x grows large
- p = 0 Means the function is a straight line (y = 1)
- p < 0 Means the function is concave up, and approaches 0 as x grows large
Limit for a Power Function
![]()
The limit of the power of a function is the power of the limit of the function, where p is any real number. (See: Properties of limits).
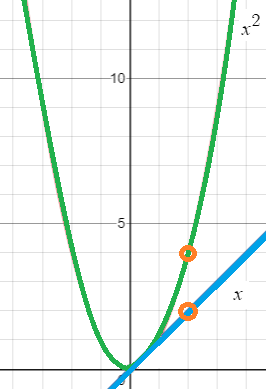 Example: Find the limit of the function f(x) = x2 as x→2.
Example: Find the limit of the function f(x) = x2 as x→2.
- Temporarily remove the power: f(x) = x
- Find the limit of (1) at the given x-value: lim = 2, using direct substitution.
- Put the power back in and solve: 22 = 4
What is the Power Rule?
The Power Rule is surprisingly simple to work with: Place the exponent in front of “x” and then subtract 1 from the exponent. For example, d/dx x3 = 3x(3 – 1) = 3x2.
The formal definition of the Power Rule is stated as “The derivative of x to the nth power is equal to n times x to the n minus one power,” when x is a monomial (a one-term expression) and n is a real number. In symbols it looks as follows:
d/dx xn = nxn – 1.
Differentiate Exponents: Examples
With the power rule, you can quickly move through what would be a complex differentiation in seconds without the aid of a calculator. Take the derivative of x1000 for example. Attempting to solve (x + h)1000 would be a time-consuming chore, so here we will use the Power Rule.
Step 1: Find “n”, which is the exponent. For this problem, n is equal to 1000.
Step 2: Substitute the value “n” into the front of the base to get 1000x1000.
Step 3: Subtract 1 from the exponent:
1000x1000-1 = 1000x999
That’s it!
Proof of the Power Rule
In order to understand how the proof of the power rule works, you should be familiar with the binomial theorem (although you might be able to get away with not knowing it if your algebra skills are strong). You’ll also need to be comfortable with the formal definition of a limit . If you have those prerequisites, it should be very easy to follow.
This proof of the power rule is the proof of the general form of the power rule, which is:
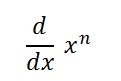
In other words, this proof will work for any numbers you care to use, as long as they are in the power format.
Example problem: Show a proof of the power rule using the classic definition of the derivative: the limit.
Step 1: Insert the power rule into the limit definition:
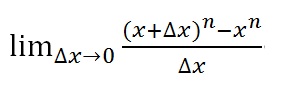
Step 2: Use the binomial theorem to evaluate the equation from Step 1:
![]()
Note: I included “…” to indicate this is an incomplete series. In order to prove the power rule you don’t need to write out the entire series.
Step 3: Simplify the equation from Step 2 using algebra. Basically, you’re canceling out any +nn and -nn, and dividing by δx:

Step 4: Expand the equation, using combinations (n choose 1):
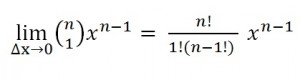
Note that you can delete any terms that multiply by Δx (because Δx is such an insignificant amount it’s practically zero).
Step 5: Use the following rules to further reduce the equation:
- 1! reduces to one, so you can eliminate it. (The ! symbol is a factorial).
- 7! / 6! = 7 or 10!/9!= 10, so n! / n – 1! = n
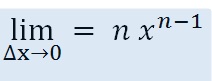
This equation is the derivative of Xn.
That’s it!
Power Rule: References
Taba, Kahlil. Lecture Notes: Power Functions. Orange Coast College. Retrieved from http://occonline.occ.cccd.edu/online/ktaba/power_functions.htm on Feb 23, 2019
Biomath Tutorials: Power Basics. University of Arizona. Retrieved from http://www.biology.arizona.edu/biomath/tutorials/power/Powerbasics.html on Feb 23, 2019
Power Functions: Math 251 Lesson Notes. Oregon State University. Retrieved from https://oregonstate.edu/instruct/mth251/cq/FieldGuide/power/lesson.html on Feb 23, 2019