Dirichlet Function & Dirichlet Eta Function (Alternating Zeta Function)

Types of Functions >

Contents:

• Dirichlet Function
• Dirichlet Eta Function

Dirichlet Function

The Dirichlet function is defined as:


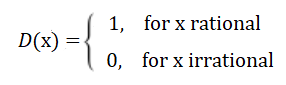
It’s a good example of a function with unusual limit behavior. At first glance, you might think that the function looks fairly simple, because it appears to neatly oscillate between zero and one. However, despite this apparent simplicity, it can’t easily be perceived. That’s because there are an infinite number of irrational numbers between every rational number. These rapid oscillations mean that the function has no limit at any real number, which also means that it isn’t a continuous function anywhere.

Modified versions of the Dirichlet function include the Popcorn Function.

The Impossible Dirichlet Function Graph

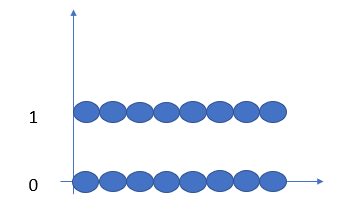
The problem of drawing a graph of the Dirichlet function stems from the fact that between every two rational numbers there is some irrational number and between every irrational number there is some rational number. Therefore, it’s impossible to draw the function’s graph because of the infinite number of jumps between 0 and 1 (Prestini, 2013). You can make a reasonable representation, which looks like lines:


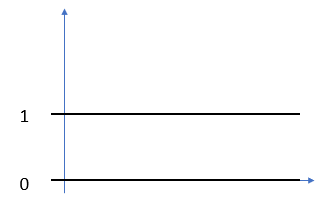
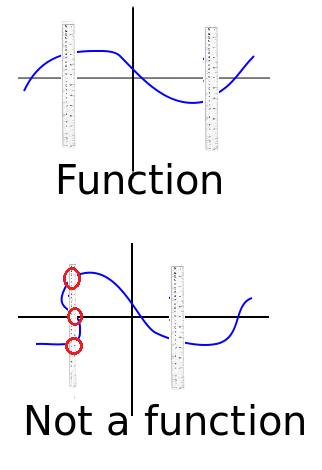
The graph, drawn like this, appears to fail the vertical line test, which would make you conclude it isn’t a function. That obviously is not correct, and the issue is that if you zoom in on the graph, it’s actually a series of very, very dense dots.

Graphs of Functions and the Vertical Line Test

The lack of a graph for the Dirichlet function is actually a very important concept in calculus. When you first start studying calculus, you’re introduced to the vertical line test to determine whether you have a function or not. However, the ability to draw a graph (or not) actually has nothing to do with the definition of a function: if a graph exists, then you can apply a vertical line test (which makes it fairly easy to spot a function). But if you can’t draw a graph (as with the Dirichlet function) that doesn’t mean it isn’t a function. All it means is that you can’t apply the vertical line test.

Dirichlet Eta Function

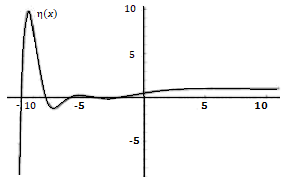
The Dirichlet Eta Function (sometimes called the zeta alternating series or the Euler zeta function) is defined by the following equation:

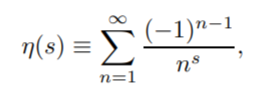
Connections to Other Functions

The Dirichlet Eta function is an alternating sign version of the Riemann zeta function, and has the same non-trivial zeros. The functional relationship between the two (Aiken, 2019) is:

η(z, 1) = (1 – 2 ^{1 – z} ) ζ (z, 1).

Other functions are closely connected with the Dirichlet eta function, including the Hurwitz-Euler eta function (which is an alternating sign version of the Hurwitz zeta function). Specifically, for x = 0, η (z, x + 1) the Hurwitz-Euler eta function becomes the eta function. The Dirichlet eta function is also a special case of the polylogarithm function.

History and Uses

The Dirichlet eta function was first investigated by Leonhard Euler who used the notation M(s). It is used mainly in number theory, particularly in studying the distribution of prime numbers and as an equivalent for the Riemann Hypothesis.

Numerous authors have used the function to explore the Riemann hypothesis, including Ronald L. Fox, who surmised that:

“Numerical display of the behavior of t strings originating inside the critical strip for the Dirichlet Eta function provides strong visual evidence for why the Riemann hypothesis is most likely true”.

Dirichlet Function: References

Aiken, E. (2019). Modified Commutation Relationships from the Berry-Keating Program.
Bagdasaryan, A. (2010). An Elementary and Real Approach to Values of the Riemann Zeta Function from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.771.3064&rep=rep1&type=pdf
Fox, R. (2019). A Conjecture Regarding the Riemann Hypothesis.
Gourdon, X. & Sebah, P. (2004). The Riemann Zeta-function ζ(s) :
generalities. Numbers, constants and computation. Retrieved December 7, 2019 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.
Hu, S. & Kim, M. (2015). THE (S, {2})-IWASAWA THEORY.
Hu, S. & Kim, M. (2019). On Dirichlet’s Lambda Function.
Larson, R. & Edwards, B. (2008). Calculus of a Single Variable. Cengage Learning.
Prestini, E. (2013). The Evolution of Applied Harmonic Analysis: Models of the Real World. Birkhäuser Boston.