Contents (Click to skip to that section):
1. Boxcar Function
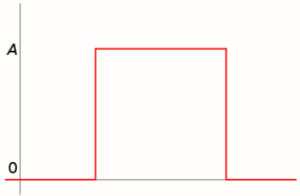
The boxcar function is a special function that has a value of zero everywhere except one single interval where it equals a constant. Its graph has the shape of a boxcar sitting on a “railway track” (the x axis).
We can write the boxcar function as:
![]()
where H is the Heaviside Step Function.
Since you can choose any constant value and any size interval, there are an infinite number of possible versions of this function.
Applications of Boxcar Functions
The simple versatility of this function makes it important for a wide variety of applications. It is especially useful in computer science, signal analysis and other engineering applications.
For example, in signal analysis, multiplying the boxcar function by the signal gives a representation of what happens when the signal is turned on for a brief period of time and then turned off.
Rectangular Function
The rectangular function (also called the rectangle function, gate function, or window function) is a special case of the boxcar function. Its graph that looks like a rectangular box centered over the y axis.
Note: A “rectangular equation” is a loosely-defined term that usually refers to a run-of-the mill function written in rectangular form (Cartesian form). In other words, the usual x, y format). It has nothing to do with the rectangular function defined here.
The rectangular function is important in electric engineering, simulation, data processing and many other fields. It can be used to check how a system responds to a sudden input. It is also often used to model probability, as a probability density function (PDF). When a PDF is equal to the probability function, it is a special case of the continuous uniform distribution. This PDF would be useful in situations where an event is likely to happen only over a single well defined interval; with a lesser chance of happening right at the borderline.
The characteristic function of this PDF is
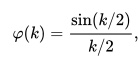
This is an alternative way of describing the PDF, and it describes it completely.
Unit Rectangle (Pulse Function)
The unit rectangle function, also called the pulse function, is a special case of the boxcar function. It is defined as:
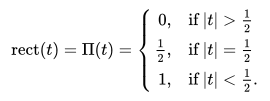
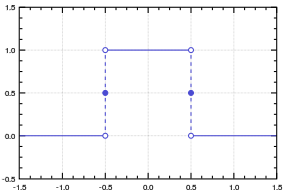
It has the shape of a 1 x 1 boxcar, centered at the origin.
References
De Oliveira, Mauricio. Continuous-time Signals (aka Analog Signals). MAE 143A Lecture Notes. Retrieved from http://control.ucsd.edu/mauricio/courses/mae143a/lectures/1analogsignals.pdf on Feb 2, 2019.
Hrynkiewicz E. (2011) 2 Rectangular Function Π(x) and Its Application for Description of Some Logical Devices Operation. In: Adamski M., Barkalov A., Węgrzyn M. (eds) Design of Digital Systems and Devices. Lecture Notes in Electrical Engineering, vol 79. Springer, Berlin, Heidelberg. Retrieved from https://link.springer.com/chapter/10.1007/978-3-642-17545-9_2 on August 26, 2019
de Oliveira, Mauricio. Continuous-time Signals (AKA analog signals).From MAE 143 A – Signals & Systems – Lecture Notes. Published online Winter 2011. Retrieved from http://control.ucsd.edu/mauricio/courses/mae143a/lectures/1analogsignals.pdf on August 26, 2019
Yen-Ping Shih and Chyi Hwang. Application of block pulse functions in dynamic simulation. Computers & Chemical Engineering Volume 6, Issue 1, 1982, Pages 7-13. Retrieved from https://www.sciencedirect.com/science/article/pii/0098135482800021 on Feb 2, 2019.