Contents:
Inner Function
Outer Function
What is an Inner Function?
An inner function is a function nested inside another function. For example, the following image shows an inner function of x2 – 3, which is nested inside the square root function:
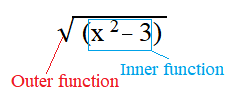
When two functions are nested like this, they are called a composite function and are a result of a chaining process that blends the two functions together. The inner function’s output becomes the outer function’s input.
The words “inner” and “outer” stem from the fact that (perhaps obviously), one function is on the inside, and another is on the outside. If you look at enough composite functions, it gets easier to see which is which. For example:
- e(x + 5) (inner = x + 5)
- √ (5x + 2) (inner = 5x + 2).
Written this way, f(g(x)), it’s fairly plain to see that the “f” function is on the outside and the “g” function is on the inside. Another valid way to write composites is (f ∘ g)(x), with the outer function coming first (in this case, f). However, in that form it isn’t clear that inner or outer functions exist at all!
In calculus, the terms “f(x)” and “g(x)” are used to denote the outer function, and the inner function, respectively. This is a custom though, and not a hard and fast rule; You might see other notation.
Example 1
For the function f(x) = (x2 – 3 · x +9 )7 , the inner function is g(x) = (x2 – 3 · x +9 ). The outer function is f(x) = x7.
Example 2
For the function f(x) = e(x · cos(x)) , the outer function is f(x) = e(x) and the inner function is g(x) = x · cos(x).
Outer Function: Definition
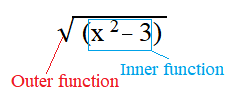
An outer function is the function (perhaps not surprisingly) on the “outside” of a composite function. Usually, whenever you see a composite function with f and g, f will be the outer function and g the inner function: For example, if your composite function is f(g(x)), then g is the inner function and f is the outer function.
Examples of Outer Function
| Function | Outer function | Inner function |
| F(x) = (x3 – 4x + 10)10 | f(x) = (x)10 | g(x) = x3 – 4x + 10 |
| F(x) = e(x cos(2x)) | f(x) = e(x) | g(x) = x cos(2x) |
| y = (5x – 4)3 | y = (x)3 | u = 5x – 4 |
Note that for the last example in the list, I used y and u instead of f and g. Think of “f” and “g” as placeholders, not absolutes. So technically, you can give them any variable name you want to (although convention states that f and g are easily recognized and commonly used). What’s important is the equation on the right hand side of the equals sign, and whether or not you correctly identify that part as inner/outer. Using the chain rule requires you to keep track of the inner and outer functions, but it doesn’t require you to label them as f/g/h or whatever (although your instructor might insist you do so!).
You might not always see parentheses, so you’ll have to figure out where to place them yourself. For example: ln sin x could be rewritten as ln (sin x), so ln(x) here is the outer function and sin x the inner function. A trickier example is:
sin2 ex.
The square (2) might throw you off, but all that’s happening here is that a squaring operation is being applied to the outer function (sin).
Sometimes you’ll see composite functions written like this: (f ∘ g)(x). Although that’s still a valid way to write them, it isn’t easy to see which in “inside” and which is “inside”. You’re more likely to see it written f(g(x)), but if you do come across the circle notation, the first function (the f in “f ∘ g”) is usually the outer function.
Related Articles
Chain Rule Examples
Function Composition and Decomposition
References
Larson, R. & Edwards, B. (2011). Calculus I with Precalculus. Cengage Learning.
Stewart, J. (2015). Single Variable Calculus, Volume 1. Cengage Learning.