A cofunction is a complementary function that typically describes two functions with complementary angles. Cofunctions can be applied to all of the trigonometric functions. For example:
Notice the “co” prefix: that indicates the function is a cofunction. This terminology dates back to 1620, when Edmund Gunter used the word co.sinus in his Canon triangulorum. The word was modified by John Newton (1658) into cosinus although the word cosine also appeared in a 1635 text by John Wells [1].
Here is a more formal definition:
If a function f is a cofunction of g, then the output of function g when evaluated at a particular angle will be equal to the output of f when evaluated at the angle complementary to that (complementary angles are two angles whose sum is 90°).
So if f is a cofunction of g, f(A) = g(B) whenever A and B are complementary angles.
Examples of Cofunction Relationships
You can see the cofunction identities in action if you plug a few values for sine and cosine into your calculator.
- The sine of ten° is 0.17364817766683; and this is exactly the same as the cosine of 80°. Note that 10° + 80° = 90°; they are complementary angles.
- The sine of 20° is 0.34202014332567; which is the same as the cosine of 70°.
- The sine of 30° is 0.5, as is cosine of 60°.
You can see this graphically if you graph the two cofunctions, sine and cosine, on the same graph. They look like the same function, just shifted along the x axis.
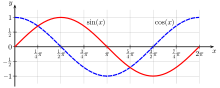
Unpacking Complementary Angles
Complementary angles are angle pairs whose sum adds up to a right angle: 90°, or π/2 radians. That makes the complementary angle to a 20 degree angle:
90 – 20 = 70 (because 70 + 20 = 90).
Similarly, the complementary angle of a π/6 angle is π/3 = (2π)/6, because (2π)/6 + π/6 = (3π)/6 = π/2.
The Cofunction Identities
The cofunction identities simply tell us the relationships between sine, tangent, and secant and their cofunctions:

References
[1] Earliest Known Uses of Some of the Words of Mathematics (C).
Sum and Difference Formulas. Retrieved from https://www.alamo.edu/contentassets/35e1aad11a064ee2ae161ba2ae3b2559/analytic/math2412-sum-difference-indentities.pdf on January 27, 2018.
Summary of Trigonometric Identities. Retrieved from https://www2.clarku.edu/faculty/djoyce/trig/identities.html on January 27, 2018.