An objective function is part of a linear programming optimization strategy, which finds the minimum or maximum of a linear function.
Linear Programming Objective Function
When a linear function z = ax + by is maximized (i.e. when you find the function’s maximum point) it’s called a linear objective function, where:
- a and b are constants,
- x and y are called “decision variables”.
The variables, which must be non-negative, satisfy a set of inequalities (constraints). For example:
- a1 x + b1 y ≤ d1
- a2 x + b2 y ≤ d2
The constraints determine the set of feasible solutions. If a linear programming problem has a solution, the optimal solution is at a vertex (corner) of the set of feasible solutions (Larson & Hodgkins, 2012). For example, the following graph shows a set of feasible solutions:
The optimal solution for a linear programming problem is always at a vertex, although there may be more than one optimal solution at multiple vertices. All you have to do is test x at each vertex.
How to Solve a Linear Programming Problem
The general steps (Larson & Hodgkins, 2012) are:
- Sketch the region bounded by the constraints,
- Find the vertices,
- Test the objective function at each vertex.
If the region is bounded, like the image above, it will have a maximum and a minimum. An unbounded region may or may not have an optimal solution. If it exists, it will be at a vertex.
Example problem: Find the maximum value of z = 2x + 2y with constraints:
- x + 2y ≤ 4,
- x – y ≤ 1.
Step 1: Sketch the region. We know that x and y are both greater than zero, so the entire graph will be in the first quadrant. Drawing the two equations (constraints) gives the shape:
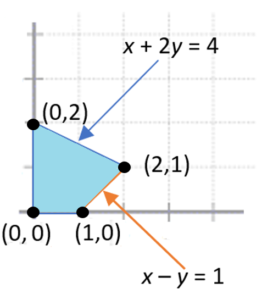
Step 2: Find the vertices. From the image, the vertices are (0, 0), (1, 0), (2, 1), (0, 2).
Step 3: “Test” each vertex by inserting them into the given function. That gives four values for the objective function:
- At (0, 0): z = 2(0) + 2(0) = 0
- At (1, 0): z = 2(1) + 2(0) = 2
- At (2, 1): z = 2(2) + 2(1) = 6
- At (0, 2): z = 2(0) + 2(2) = 4
The greatest value here is 6, so the maximum for z occurs at (2, 1).
References
Disha Experts (2013). 10 in One Study Package for CBSE Mathematics Class 12 with Objective Questions & 3 Sample Papers 3rd Edition. Disha Publications.
Larson, R. & Hodgkins, A. (2012). College Algebra with Applications for Business and Life Sciences. Cengage Learning.