Contents:
What is an Integrable Function?
Generally speaking, if a function is integrable, all it means is that the integral is well defined and continuous.
Functions that are easily integrable include continuous functions, power functions, piecewise continuous functions, and monotonic functions.
Some types of functions with discontinuities , turns or other odd behavior may also be integrable— depending on the type and number of discontinuity. If the discontinuity is removable, then that function is still integrable. For example, the absolute value function y = |x| is integrable, even though x = 0 is undefined.
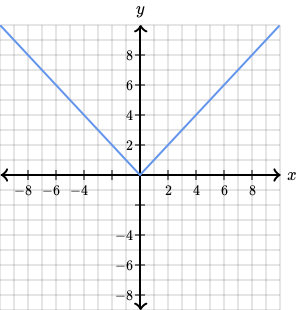
What is a Non Integrable Function?
Non integrable functions do not have well defined integrals. These may involve discontinuities that aren’t removable, like Oscillating Discontinuities or Essential Discontinuities (Second Type or Irremovable Discontinuity). Non integrable functions also include any function that jumps around too much, as well as any function that results in an integral with an infinite area.
Two basic functions that are non integrable are y = 1/x for the interval [0, b] and y = 1/x2 for any interval containing 0.
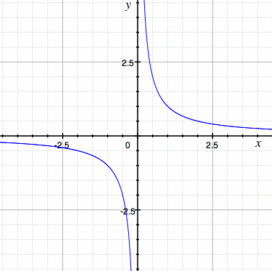
When mathematicians talk about integrable functions, they usually mean in the sense of Riemann Integrals. A Riemann integral is the “usual” type of integration you come across in elementary calculus classes. It’s the idea of creating infinitely small numbers of rectangles under a curve. However, there is another type of integration that can integrate even the most pathological of functions: Lebesgue Integration. This is usually tackled in more advanced mathematics classes.
Locally Integrable Functions
Implications of Local Integrability
The condition of being a locally integrable function implies that the function’s indefinite integral is locally absolutely continuous, but while all continuous functions are locally integrable (Al-Omari, 2014), the converse isn’t true: a locally integrable function isn’t necessarily continuous (although in many cases they are).
In addition, the absolute value of a locally integrable function is locally integrable (Debnath & Mikusinski, 2005). However, just because a function is locally integrable doesn’t mean that the derivative there is also locally integrable (Park & Regensburger, 2011).
Formal Definition of Locally Integrable Function
More formally, a locally integrable function is defined as a bounded function (i.e. a function with and interval consisting of an upper bound or lower bound), rather than having infinite bounds (i.e. bounds of -∞, ∞). This can be written as follows:
“A Locally integrable function is a function f defined on ℝ such that for any compact interval [a, b], the integral
exists” ~ David Hilbert.
References
Al-Omari, S. On a Widder potential transform and its extension to a space of locally integrable Boehmians. Journal of the Association of Arab Universities for Basic and Applied Sciences Volume 18, 2015 – Issue 1.
Australian Mathematical Sciences Institute. Functions integrable and not. Retrieved November 23, 2019 from: https://amsi.org.au/ESA_Senior_Years/SeniorTopic3/3f/3f_5appendix_3.html
Bietcher, (2010). Integration – A Functional Approach. Springer Science & Business Media.
Debnath, L. & Mikunsinski, P. (2005). Introduction to Hilbert Spaces with Applications 3rd Edition. Academic Press.
Hilbert, D. (2008). A quick look at topological and functionalspaces.
Park, H. & Regensburger, G. Gröbner Bases in Control Theory and Signal Processing. De Gruyter. 2011.
Turner, M. & Bates, D. (Eds.) Mathematical Methods for Robust and Nonlinear Control: EPSRC Summer School. Springer London. 2007.