Calculus Definitions > Exterior calculus
Contents:
What is Exterior Calculus?
Exterior calculus is a high dimensional extension of the “usual” calculus you encounter in introductory classes. It’s a generalized type of calculus that works in every dimension, and is particularly well suited for working in complex analysis. It is widely used in many areas, including general relativity, theories of electromagnetic fields and elasticity, thermodynamics, differential geometry, and topology.
In basic calculus, the focus is on two-dimensional curves and surfaces (like arcs and circles) or three-dimensional objects (like cones or spheres). Exterior calculus focuses on a step up from 2D and 3D: higher dimensional space, where curves and surfaces are called Manifolds. This advanced calculus doesn’t reinvent the wheel though; Many familiar theorems from traditional calculus extend to exterior calculus, including the chain rule, the change of variable formula, and the Fundamental Theorem of Calculus.
Exterior calculus is considered by many authors to be a superior alternative to vector calculus, in part because of its relative simplicity.
Exterior Calculus Topics
The major topics you’ll come across in exterior calculus include:
- Differential forms: an extension of single variable calculus that works on manifolds, as well as basic curves, solids, and surfaces,
- Theorems such as the divergence theorem, Stokes’ theorem (and Stokes’ lemma),
- Fundamental operations like the interior product, exterior product, and pullbacks.
- Invariant mappings, wedge products, Lie groups, and the Lie derivative.
Exterior Derivative
The exterior derivative in exterior calculus generalizes the concept of a slope in single-variable calculus to higher degree differential forms. It is one of the most important concepts in differential manifolds (the higher dimensional equivalent of differential calculus).
The exterior derivative was first developed by French mathematician Elie Joseph Cartan (1869-1951). This calculus of p-forms, where the exterior derivative d is a basic tool, is an alternative to the traditional vector calculus, and is gradually replacing it (Cvitanović, n.d.).
Exterior Calculus Derivative and Forms
While single variable calculus centers around functions, calculus on manifolds deals with differential forms. That means the basic derivative and integral has to be extended to higher dimensions. A basic function (the type you come across in undergraduate calculus) is 0-form, and ordinary differential equations deal with 1-forms.
The idea behind exterior derivatives is that they increase the degree of a form by 1: in other words, you can apply it to any p-form to get an (p + 1) form. For example, you can apply it to a 0-form to get a 1-form. For example:
- Gradient: 0-form to 1-form,
- Curl: 1-form to 2-form (i.e. this operator maps vector fields to vector fields in three dimensions),
- Divergence: 2-form to 3-form.
Formal Definition
In exterior calculus, the exterior derivative is defined for a function f(x, y, z) as:
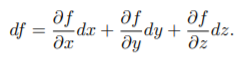
The entire expression df is a 1-form and the operator d is the exterior derivative.
References
Bachman, D. (2012). A Geometric Approach to Differential Forms. Springer Science & Business Media.
Cvitanović, P. Chapter 11. Differential Calculus on Manifolds. Center for Nonlinear Science – Georgia Institute of Technology. Retrieved January 5, 2019 from: http://www.cns.gatech.edu/~predrag/courses/PHYS-6124-12/StGoChap11.pdf
Greub, W. (1972). Connections, Curvature, and Cohomology V1: De Rham cohomology of manifolds and vector bundles. Academic Press.
Wheeler, J. Exterior Calculus. Retrieved January 5, 2019 from: http://www.physics.usu.edu/Wheeler/GaugeTheory/09Jan12zNotes.pdf
Story, T. (2005). Introduction to Differential Geometry with applications to Navier-Stokes Dynamics. iUniverse, Inc.
Tu, L. (2010). An Introduction to Manifolds. Springer Science & Business Media.