Contents (Click to skip to that section):
1. Cosecant Function
The cosecant function, csc(x) or 1/sin(x), is the reciprocal of the sine function, sin(x). In other words, if you flip the fraction sin(x)/1 upside down, you get the cosecant function.
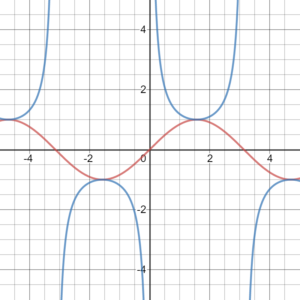
This is a periodic function, which repeats every 2π periods.
Properties
- Domain: x ∈ ℝ* except for x = kπ, where k = …-3, -2, -1, 0, 1, 2, 3, …
- Range: y ∈ (-∞, -1] ∪ [1, ∞)
- Continuity: This is a continuous function.
- Boundedness: This is an unbounded function.
- Extrema: The cosecant function has local minimums at x = π / 1 + 2kπ, and local maximums at x = 3π / 2 + 2kπ, where k = …-3, -2, -1, 0, 1, 2, 3…
If you’re unfamiliar with set notation:
- *ℝ = the set of real numbers,
- ∈ = “is in the set of”
- ∪ = “the union”. In other words, both of the two specified sets.
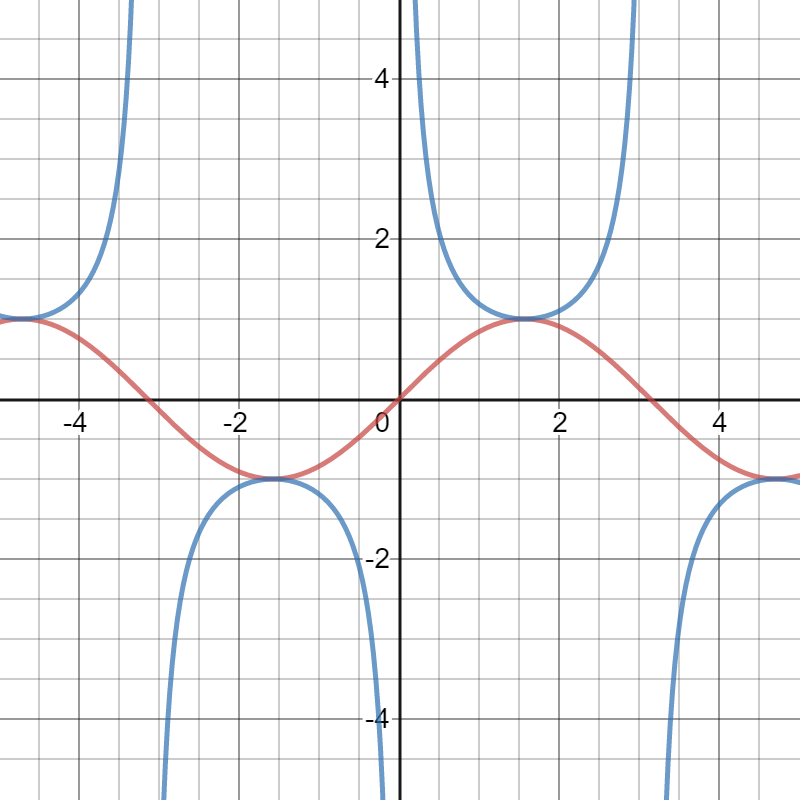
Graph of the Cosecant Function
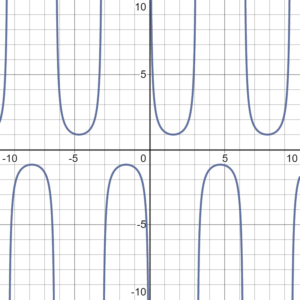
A few properties of the cosecant function graph:
- The function is not defined at any multiple of π, which means that the vertical asymptotes for the cosecant function occur at every multiple of π. This is the same place where the reciprocal function, sin(x), has zeros.
- This function has no roots (it never crosses the x-axis).
- The cosecant function is an odd function, which means it is symmetrical around the origin (e.g. 0).
Complementary to Secant
The cosecant function is the complementary function (the cofunction) to the secant function. An example of how this works:
- The secant of 10° is 1.0154.
- The cosine of 80° is 1.0154.
Note that 10° + 80° = 90; they are complementary angles. If you use any combination of angles for the secant and cosecant, they will have the same result as long as the two angles add up to 90 degrees.
2. Inverse Cosecant Function
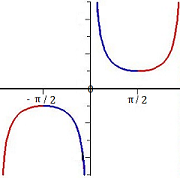
The inverse cosecant function (Csc-1x or Arccsc x) is the inverse function of the domain-restricted cosecant function, to the half-open interval [-π/2, 0) and (0, π/2} (Larson & Falvo, 2016).
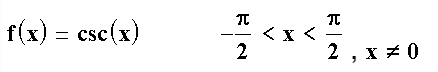
In some texts, you might see the domain of the cosecant function restricted to ∈ (0, π/2] ∪ (π, 3π/2].
The domain of the inverse secant function is (−∞, −1] ∪ [1, +∞).
Why Restrict the Domain?
The inverse cosecant function is an inverse function, which has to follow certain rules. The most important rule is that in order for an inverse function to exist for any particular function, that function must be one-to-one. One to one functions map one element of the domain to one element of the range, and they must be either continually decreasing or continually increasing.
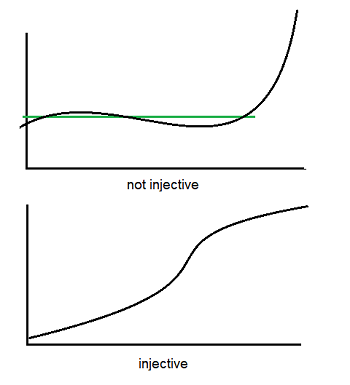
If you take a look at the graph of the cosecant function, it’s clearly not one-to-one, if you consider the entire domain.
So, restricting the domain of the cosecant function into a small segment that is either increasing or decreasing is the only way to find an inverse.
3. Excosecant Function
The excosecant function is defined in terms of the cosecant function (csc):
excosecant (θ) = excsc (θ) = csc θ – 1
The Obsolete Excosecant Function
The excosecant function is one of a multitude of archaic functions (including the haversine function and exsecant Function) that were once popular in astronomy, surveying, and navigation when tables were widely used.
The function fell out of favor for a few reasons. An understanding of calculus (and in particular, differential equations) resulted in all trigonometric functions being defined in terms of the sine function and cosine function (along with rational functions and linear coordinate changes). In addition, most of the dozens of archaic functions can now be calculated directly (with calculators or computers) instead of using tables, making them essentially obsolete.
Meaning of the Excosecant Function
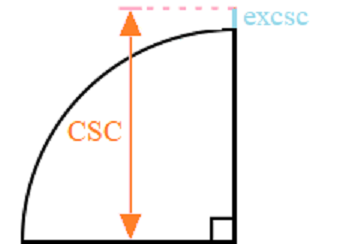
The name “excosecant” is a contraction of the words exterior and cosecant: it tells you the portion of the cosecant line that lies outside of the unit circle. The unit circle has a radius of 1, so all you need to do to find the excosecant is:
- Find the cosecant,
- Subtract 1.
References
Hall, A. & Frink, G. (1909). Plane Geometry. Henry Holt.
Desmos.com (graph)
Larson, R. & Falvo, D. (2016). Precalculus. Cengage Learning.