What is a Bump Function?
A bump function (sometimes called a test function) is, perhaps not surprisingly, a function with a “bump.” A simple example is the real-valued function
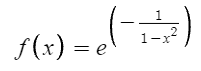
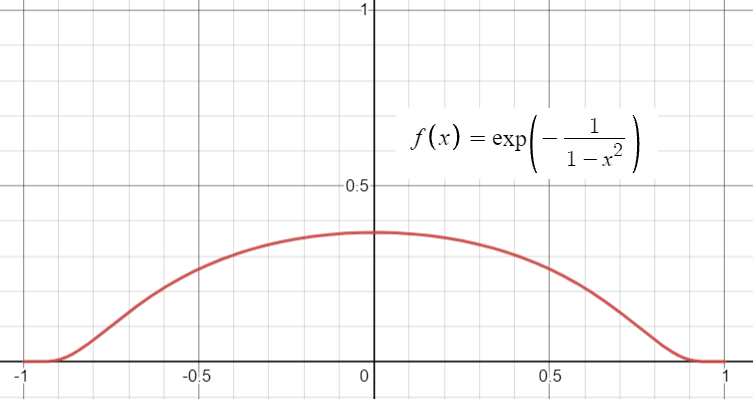
The function is defined on the open interval (-1, 1), otherwise it equals zero.
More precisely, a bump function is a smooth function with compact support. Compact support means that the function is zero outside of a compact set. Bump functions are also usually (i.e., there are exceptions) non-negative everywhere, have outputs no more than 1, and equal 1 on the defined compact set [1]. In a sense, they are the smooth analogues of characteristic functions [2].
Example of Bump Function Uses
Bump functions have a variety of uses in math, including use as mollifiers (smooth functions with special properties), as smooth cutoff functions, or to create smooth partitions of unity. Specific examples include:
- Creating smooth partitions of unity and to extend locally defined smooth functions to globally defined smooth functions [3].
- Functions created in Euclidean space can be used to construct bump functions on any smooth manifold (where support is prescribed as “equal to one region” [1]. Generalization to higher dimensions can be done with polar coordinates [4].
- The Hicks-Henne bump function is used in aerodynamics. For example, to model uncertainties on an airfoil’s geometries[5].
- Keane’s bump function is a standard benchmark for nonlinear constrained optimization [6].
References
Graph created with Desmos.
Bump Function Image: Joshdif|Wikimedia Commons. CC 4.0.
[1] Wang, Z. Lecture 3: Smooth Functions. Retrieved October 19, 2021 from: http://staff.ustc.edu.cn/~wangzuoq/Courses/18F-Manifolds/Notes/Lec03.pdf
[2] Bump Functions, part 1. The Unapologetic Mathematician. Retrieved October 19, 2021 from: https://unapologetic.wordpress.com/2011/03/12/bump-functions-part-1/
[3] Fry, R. & McManus, S. (2002). Smooth Bump Functions and the Geometry of Banach Spaces. Retrieved October 19, 2021 from: https://core.ac.uk/download/pdf/81972936.pdf
[4] A more intuitive way of constructing bump functions. Fruits of Procrastination. Retrieved October 19, 2021 from: https://randommathgenerator.com/2020/03/14/a-more-intuitive-way-of-constructing-bump-functions/
[5] Palar, P. Hicks-henne bump function. Retrieved October 19, 2021 from: https://www.mathworks.com/matlabcentral/fileexchange/49560-hicks-henne-bump-function
[6] Mishra, S. Minimization of Keane’s Bump Function by the Repulsive Particle Swarm and the Differential Evolution Models. Retrieved October 19, 2021 from: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=983836