Quintic Function (Polynomial)

What is a Quintic Function?

A quintic function, also called a quintic polynomial, is a fifth degree polynomial. “Quintic” comes from the Latin quintus, which means “fifth.” The general form is:

y = ax⁵ + bx⁴ + cx³ + dx² + ex + f

Where a, b, c, d, and e are numbers (usually rational numbers, real numbers or complex numbers);

The first coefficient “a” is always non-zero, but you can set any three other coefficients to zero (which effectively eliminates them) and it will still be a quintic. For example:

f(x) = 9x⁵ + 10x + 2.
f(x) = x⁵ − 4x + 21.

These are still quintic functions because the highest degree of the polynomial (i.e. the largest exponent) is 5.

Quintic polynomials do not have any general symmetry. They do have:

Zero to four extrema. “Extrema” are maximums and minimums of graphs. They can be overall highs and lows (global maximums and global minimums) or highs and lows on portions of the graph (local maximums and local minimums).
One to three inflection points. “Inflection points” are places where the graph changes in shape (curvature) from concave up to concave down.
One to five roots (zeros). A “root” is where the graph crosses the x-axis. Exact roots cannot be found with a formula (unlike the roots of a second degree polynomial, which can be found with the quadratic equation).

Examples of Quintic Polynomials

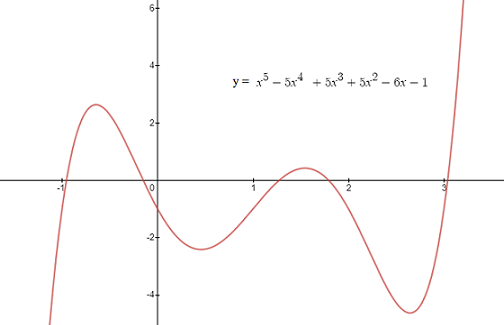
The following quintic function has a graph with well-defined highs and lows. You can think of it as a “classic” type of quintic, which is a good visual representation of the function. Characteristics include:

Five roots,
Four distinct extrema (two local maximums and two local minimums),
Very distinct, collinear, inflection points (“collinear means that they can be joined by one straight line).

quintic function

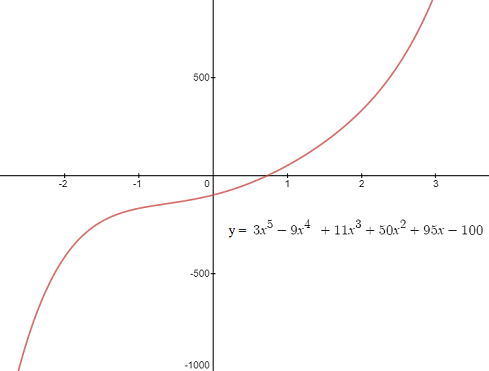
Quintic functions don’t have to have such a well defined graph though. The following function is a quintic that is fairly flattened:
quintic polynomial

Derivative of a Quintic Function

The derivative of a quintic function is a quartic function. As an example, the derivative of:

f(x) = x⁵ − 4x + 2 = 0

…using the power rule, is

f′ = 5x⁴ − 4

Uses

Quintic functions are fairly common in calculus and have many practical uses in fields like hydrodynamics, computer graphics, optics and spatial analysis.

References

Andrilli, A. et al. (2003). Elementary Linear Algebra. Gulf Professional Publishing.
Calculus Quest. Retrieved December 3, 2019 from: https://oregonstate.edu/instruct/mth251/cq/FieldGuide/polynomial/ex.2a.html
Davidson, J. (1998). Fifth Degree Polynomials. Retrieved December 3, 2019 from: https://www.sscc.edu/home/jdavidso/Math/Catalog/Polynomials/Fifth/Fifth.html
Graphs: Desmos.com