What is the Error Function?
The error function (erf) is a special function which gets its name for its importance in the study of errors. It is sometimes called the Gauss or Gaussian Error Function and occasionally a Cramp function [1].
As well as error theory, the error function is also used in probability theory, mathematical physics (where it can be expressed as a special case of the Whittaker function), and a wide variety of other theoretical and practical applications. For example, Fresnel integrals, which are derived from the error function, are used in the theory of optics.
In probability and statistics, the function integrates the normal distribution (aka Gaussian Distribution). It gives the probability that a normally distributed random variable Y (with mean 0 and variance ½), falls into the range [−x, x].
Formula and Properties
The error function is defined by the following integral:
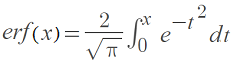
The function has the following four properties:
- erf (-∞) = -1
- erf (+∞) = 1
- erf (-x) = -erf (x)
- erf (x*) = [erf (x)]*
(* is a complex conjugate, where the real and imaginary parts are equal in magnitude but opposite in sign. For example, a + bi → a – bi)
Graph of the Error Function
The error function is an odd function, which means it is symmetric about the origin.
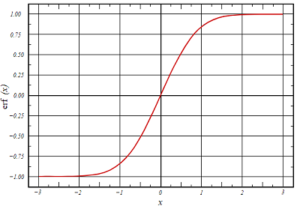
Table of Values
For a full list of the table of values, download this pdf [2].
Approximation for Erf
If you have a programmable calculator, the following formula which serves as a good approximation to the function. It’s accurate to 1 part in 107 [3].
erf(z) = 1 – (a1 T + a2 T2 + a3 T3 + a4 T4 + a5 T5 )
) e-z2
Where:
- T = 1 / (1 + (0.3275911 * z)),
- Z = a z-score
- a1 = 0.254829592
- a2 = -0.284496736
- a3 = 1.421413741
- a4 = -1.453152027
- a4 = 1.061405429
References
[1] Cramp Function. Retrieved March 9, 2022 from: https://p-distribution.com/cramp-function-distribution/
[2] Washington State University. Error Function. Retrieved November 27, 2019 from: http://courses.washington.edu/overney/privateChemE530/Handouts/Error%20Function.pdf
[3] Cheung. Properties of … erf(z) And … erfc(z). Retrieved November 27, 2019 from: http://www.sci.utah.edu/~jmk/papers/ERF01.pdf