Total Function & Partial Function: Definition

Types of function > Total Function & Partial Function

Contents:

1. What is a Total Function?
2. What is a Partial Function?

What is a Total Function?

In general, a total function is usually just another name for a regular function. The use of the term is to make it clear that the function is defined for all elements in its domain, compared to partial functions which are only defined for part of the domain. If there’s any chance a reader might interpret a function as being a partial function (or something else entirely), an author will usually state it’s a “total” function to avoid misinterpretation.

In notation, if dom f = A, then f is a total function on A (Dean, 1997).

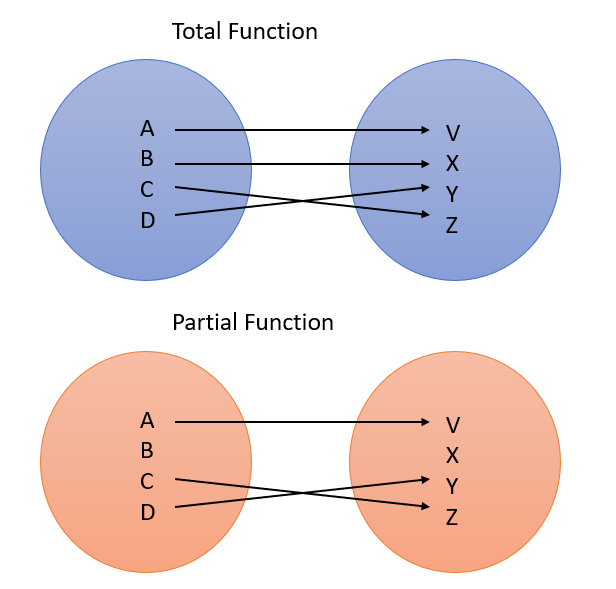
Total Function Examples

Many “usual” functions are total functions, including the exponential function, the square function, and general polynomial functions. The empty function is (perhaps surprisingly) also a total function. Even though there are technically no members in the set, the function is still defined for its whole domain.

The reciprocal function f(X) = 1/x is not a total function on the set of real numbers, because it isn’t defined for “0”.

What is a Partial Function?

A partial function is a function that only partially works.

A function usually creates one unique output for every input. For example, let’s say you have inputs A, B, and C. They might map to X, Y, and Z, as shown in the blue circle on the left: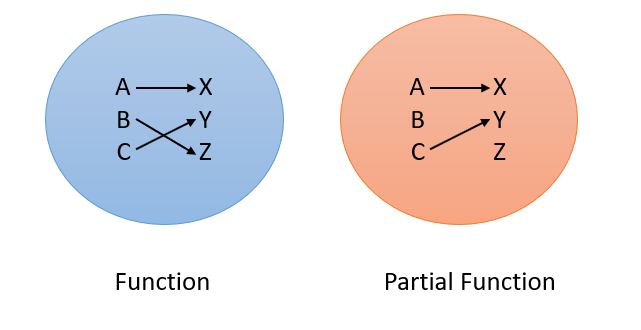

But sometimes, not every input matches to an output. Technically, if one or more inputs (e.g. x-values) aren’t “linked” to an output value (e.g. a y-value), then it’s not a function. However, there is an exception made when the function mostly works, as in the above orange circle. When this happens, the non-function is called a partial function.

What Causes a Partial Function?

When you begin calculus, you usually study functions that have real numbers (any number, including decimals and fractions, that can be represented on a number line) for inputs and outputs. However, once you start restricting your domain and range to other sets (like the set of natural numbers ℕ or rational numbers), some functions only work some of the time.

As an example, the function f(x) = x/3 is a function, and is well-defined if both your inputs and outputs are real numbers.

However, let’s say you restrict the domain to natural numbers (the counting numbers: 1, 2, 3, …). A problem happens: the function is no longer fully defined. Here’s why:

Let’s take f(x) = x/3 and input a few natural numbers:

• f(x) = 1/3
• f(x) = 2/3
• f(x) = 3/3

All of the outputs there are real numbers, so if your range is defined as “the set of all real numbers”, then the function is well defined. However, take those same inputs, and restrict the range to ℕ, and there’s a problem: the first two fractions (1/3 and 2/3) are not natural numbers, so the function is undefined there. However, the function partially works: 3/3 is in ℕ. This is why f(x) = x/3, defined with ℕ as the range, is a partial function.

References

Chapter 2. Relations, Functions, Partial Functions. Retrieved December 14, 2019 from: https://www.seas.upenn.edu/~jean/cis160/cis160slides4.pdf

References

Dean, N. (1997). The Essence of Discrete Mathematics. Prentice Hall.
Gallier, J. (2011). Discrete Mathematics. Springer Science & Business Media.