Probability and Statistics > Non Normal Distribution
Although the normal distribution takes center stage in statistics, many processes follow a non normal distribution. This can be due to the data naturally following a specific type of non normal distribution (for example, bacteria growth naturally follows an exponential distribution). In other cases, your data collection methods or other methodologies may be at fault.
Types of Non Normal Distribution
Many distributions naturally follow non normal patterns.
- Beta Distribution.
- Exponential Distribution.
- Gamma Distribution.
- Inverse Gamma Distribution.
- Log Normal Distribution.
- Logistic Distribution.
- Maxwell-Boltzmann Distribution.
- Poisson Distribution.
- Skewed Distribution.
- Symmetric Distribution.
- Uniform Distribution.
- Unimodal Distribution.
- Weibull Distribution.
Reasons for the Non Normal Distribution
Many data sets naturally fit a non normal model. For example, the number of accidents tends to fit a Poisson distribution and lifetimes of products usually fit a Weibull distribution. However, there may be times when your data is supposed to fit a normal distribution, but doesn’t. If this is a case, it’s time to take a close look at your data.
- Outliers can cause your data the become skewed. The mean is especially sensitive to outliers. Try removing any extreme high or low values and testing your data again.
- Multiple distributions may be combined in your data, giving the appearance of a bimodal or multimodal distribution. For example, two sets of normally distributed test results are combined in the following image to give the appearance of bimodal data.
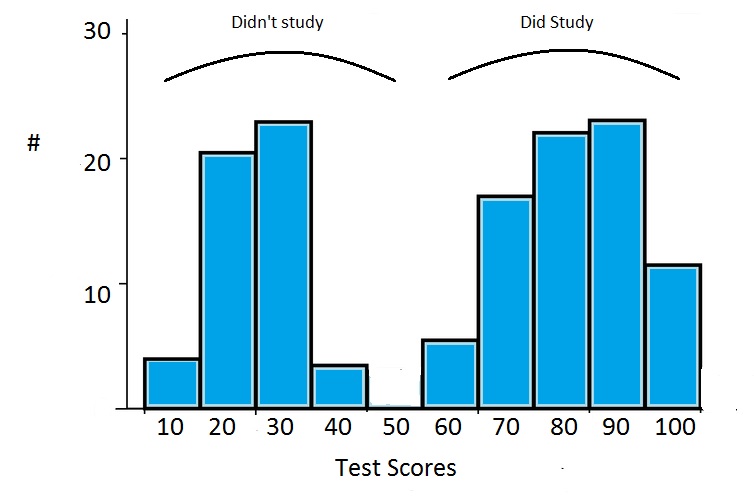
- Insufficient Data can cause a normal distribution to look completely scattered. For example, classroom test results are usually normally distributed. An extreme example: if you choose three random students and plot the results on a graph, you won’t get a normal distribution. You might get a uniform distribution (i.e. 62 62 63) or you might get a skewed distribution (80 92 99). If you are in doubt about whether you have a sufficient sample size, collect more data.
- Data may be inappropriately graphed. For example, if you were to graph people’s weights on a scale of 0 to 1000 lbs, you would have a skewed cluster to the left of the graph. Make sure you’re graphing your data on appropriately labeled axes.
Dealing with Non Normal Distributions
You have several options for handling your non normal data. Many tests, including the one sample Z test, T test and ANOVA assume normality. You may still be able to run these tests if your sample size is large enough (usually over 20 items). You can also choose to transform the data with a function, forcing it to fit a normal model. However, if you have a very small sample, a sample that is skewed or one that naturally fits another distribution type, you may want to run a non parametric test. A non parametric test is one that doesn’t assume the data fits a specific distribution type. Non parametric tests include the Wilcoxon signed rank test, the Mann-Whitney U Test and the Kruskal-Wallis test.
See also:
- How to Use Chebyshev’s Theorem (Video)
- How to Use Slovin’s Formula (video)
- The Mean of the Sampling Distribution for a Proportion.
References
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.