Contents:
- Definition of a Probability Distribution
- Probability Distribution Table Definition
- A to Z List of Distributions
What is a Probability Distribution?
A probability distribution tells you what the probability of an event happening is. Probability distributions can show simple events, like tossing a coin or picking a card. They can also show much more complex events, like the probability of a certain drug successfully treating cancer.
There are many different types of probability distributions in statistics including:
- Basic probability distributions which can be shown on a probability distribution table.
- Binomial distributions, which have “Successes” and “Failures.”
- Normal distributions, sometimes called a Bell Curve.
The sum of all the probabilities in a probability distribution is always 100% (or 1 as a decimal).
Ways of Displaying Probability Distributions
Probability distributions can be shown in tables and graphs or they can also be described by a formula. For example, the binomial formula is used to calculate binomial probabilities.
The following table shows the probability distribution of a tomato packing plant receiving rotten tomatoes. Note that if you add all of the probabilities in the second row, they add up to 1 (.95 + .02 +.02 + 0.01 = 1).
The following graph shows a standard normal distribution, which is probably the most widely used probability distribution. The standard normal distribution is also known as the “bell curve.” Lots of natural phenomenon fit the bell curve, including heights, weights and IQ scores. The normal curve is a continuous probability distribution, so instead of adding up individual probabilities under the curve we say that the total area under the curve is 1.
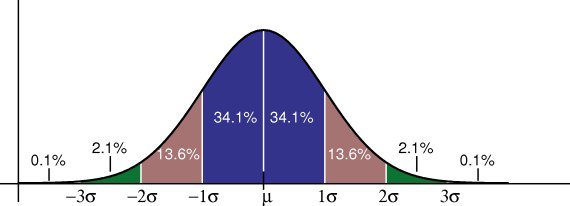
Note: Finding the area under a curve requires a little integral calculus, which you won’t get into in elementary statistics. Therefore, you’ll have to take a leap of faith and just accept that the area under the curve is 1!
Probability Distribution Table
A probability distribution table links every outcome of a statistical experiment with the probability of the event occurring. The outcome of an experiment is listed as a random variable, usually written as a capital letter (for example, X or Y). For example, if you were to toss a coin three times, the possible outcomes are:
TTT, TTH, THT, HTT, THH, HTH, HHT, HHH
You have a 1 out of 8 chance of getting no heads at all if you throw TTT. The probability is 1/8 or 0.125, a 3/8 or 0.375 chance of throwing one head with TTH, THT, and HTT, a 3/8 or 0.375 chance of throwing two heads with either THH, HTH, or HHT, and a 1/8 or .125 chance of getting three heads.
The following table lists the random variable (the number of heads) along with the probability of you getting either 0, 1, 2, or 3 heads.
| Number of heads (X) | Probability P(X) |
| 0 | 0.125 |
| 1 | 0.375 |
| 2 | 0.375 |
| 3 | 0.125 |
Probabilities are written as numbers between 0 and 1; 0 means there is no chance at all, while 1 means that the event is certain. The sum of all probabilities for an experiment is always 1, because if you conduct and experiment, something is bound to happen! For the coin toss example, 0.125 + 0.375 + 0.375 + 0.125 = 1.
Need help with a homework question? Check out our tutoring page!
More complex probability distribution tables
Of course, not all probability tables are quite as simple as this one. For example, the binomial distribution table lists common probabilities for values of n (the number of trials in an experiment).
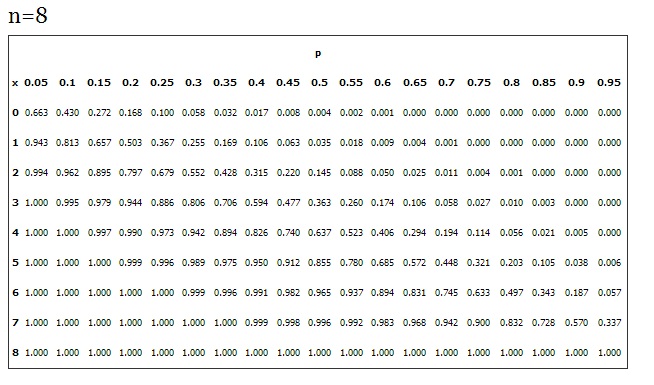
The more times an experiment is run, the more possible outcomes there are. the above table shows probabilities for n = 8, and as you can probably see — the table is quite large. However, what this means is that you, as an experimenter, don’t have to go through the trouble of writing out all of the possible outcomes (like the coin toss outcomes of TTT, TTH, THT, HTT, THH, HTH, HHT, HHH) for each experiment you run. Instead, you can refer to a probability distribution table that fits your experiment.
Check out our YouTube channel for more stats help and tips!
List of Statistical Distributions
Jump to A B C D E F G H I J K L M N O P R S T U V W Y Z.
Click any of the distributions for more information.
A
- Bates Distribution.
- Bell Shaped Distribution
- Benford Distribution: Definition, Examples
- Bernoulli Distribution
- Beta Binomial Distribution
- Beta Distribution.
- Beta Geometric Distribution (Type I Geometric)
- Beta Prime Distribution
- Binomial Distribution.
- Bimodal Distribution.
- Birnbaum-Saunders Distribution
- Bivariate Distribution
- Bivariate Normal Distribution.
- Bradford Distribution
- Burr Distribution.
- Categorical Distribution
- Cauchy Distribution.
- Chi-Bar-Squared Distribution
- Compound Probability Distribution
- Continuous Probability Distribution
- Copula Distributions
- Cosine Distribution
- Cramp Function Distribution
- Cumulative Frequency Distribution
- Cumulative Distribution Function
- Degenerate Distribution.
- De Moivre Distribution
- Dirichlet Distribution.
- Discrete Probability Distribution
- Empirical Distribution Function
- Erlang Distribution.
- Eulerian Distribution
- Exponential Distribution.
- Exponential-Logarithmic Distribution
- Exponential Power Distribution.
- Extreme Value Distribution.
- F Distribution.
- Factorial Distribution
- Fat Tail Distribution.
- Ferreri Distributions
- Fisk Distribution.
- Folded Normal / Half Normal Distribution.
- G-and-H Distribution.
- Gamma Distribution
- Gamma-Normal Distribution
- Gamma Poisson Distribution
- Generalized Error Distribution.
- Geometric Distribution.
- Gompertz Distribution.
- Gompertz-Makeham Distribution
- Half-Cauchy Distribution
- Half-Logistic Distribution
- Hansmann’s Distributions
- Helmert’s Distribution
- Heavy Tailed Distribution
- Hyperbolic Secant Distribution
- Hyperexponential Distribution
- Hypergeometric Distribution.
- Hyperbolic Distribution
- Landau Distribution
- Laplace Distribution.
- Lévy Distribution.
- Lindley Distribution.
- Location-Scale Family of Distributions
- Logarithmic Distribution
- Loglinear model / distribution
- Lognormal Distribution.
- Lomax Distribution.
- Long Tail Distribution.
- Marginal Distribution
- Mixture Distribution
- Modified Geometric Distribution
- Multimodal Distribution.
- Multinomial Distribution.
- Multivariate Distribution: Definition
- Multivariate Gamma Distributions
- Multivariate Normal Distribution.
- Muth Distribution
- Nakagami Distribution.
- Negative Binomial Distribution
- Non-Central Distribution
- Noncentral Beta Distribution
- Normal Distribution.
- Parabolic Distribution
- Pareto Distribution.
- Pearson Distribution.
- PERT Distribution.
- Phase Type Distribution
- Pólya Distribution
- Poisson Distribution.
- Power Function Distribution
- Power Law Distribution
- Power Series Distributions
- Rademacher Distribution
- Rayleigh Distribution.
- Reciprocal Distribution.
- Relative Frequency Distribution
- Rician Distribution.
- Robust Soliton Distribution
- Semicircle Distribution
- Severity Distribution
- Sine Distribution
- Skellam Distribution (Poisson Difference Distribution)
- Skewed Distribution
- Special Distribution: Definition, List of
- Stable Distribution
- Standard Power Distribution & U Power Distribution
- Symmetric Distribution
- T Distribution.
- Trapezoidal Distribution.
- Triangular Distribution.
- Truncated Normal Distribution.
- Tukey Lambda Distribution.
- Tweedie Distribution.
See also:
Birnbaum-Saunders distribution
The Birnbaum-Saunders distribution is a continuous probability distribution that was introduced by Z. W. Birnbaum and S. C. Saunders in 1969. It is a two-parameter distribution, with the parameters alpha and beta. The Birnbaum-Saunders distribution is a generalization of the Weibull distribution, and it can be used to model a variety of data sets, including data sets that are skewed or have heavy tails.
The Birnbaum-Saunders distribution is defined as follows:
f(x) = (beta * x)^(alpha – 1) * exp(-beta * x) / Gamma(alpha),
where:
f(x) is the probability density function of the Birnbaum-Saunders distribution.
x is the random variable.
alpha and beta are the parameters of the distribution.
Gamma(alpha) is the gamma function.
The Birnbaum-Saunders distribution has a number of properties that make it a useful tool for modeling data. These properties include:
The Birnbaum-Saunders distribution is flexible, and it can be used to model a variety of data sets.
The Birnbaum-Saunders distribution is robust, and it is not sensitive to outliers.
The Birnbaum-Saunders distribution is easy to estimate, and there are a number of software packages that can be used to estimate the parameters of the distribution.
The Birnbaum-Saunders distribution is a useful tool for a variety of applications, including:
Statistical modeling: The Birnbaum-Saunders distribution can be used to model a variety of data sets, including data sets that are skewed or have heavy tails.
Risk analysis: The Birnbaum-Saunders distribution can be used to model the risk of rare events, such as natural disasters or financial crises.
Decision making: The Birnbaum-Saunders distribution can be used to make decisions under uncertainty, such as decisions about how to allocate resources or how to invest money.
Overall, the Birnbaum-Saunders distribution is a versatile and powerful tool for modeling data. It is easy to estimate and use, and it can be used to model a variety of data sets.
Here are some additional details about the Birnbaum-Saunders distribution:
The Birnbaum-Saunders distribution is unimodal, with a median of beta.
The mean (μ) and variance (σ2) of the Birnbaum-Saunders distribution are given by:
μ = beta * Gamma(alpha + 1) / Gamma(alpha)
σ2 = beta^2 * Gamma(alpha + 2) / Gamma(alpha)
The Birnbaum-Saunders distribution is a special case of the Weibull distribution when alpha = 2.
The Birnbaum-Saunders distribution is a special case of the gamma distribution when beta = 1.
The Birnbaum-Saunders distribution is named after Z. W. Birnbaum and S. C. Saunders, who introduced it in 1969. Birnbaum and Saunders were interested in modeling the failure time of components under cyclic loading. They found that the Birnbaum-Saunders distribution was a good fit for the data they collected, and they proposed the distribution as a general model for failure time data.
The Birnbaum-Saunders distribution has been used in a variety of applications, including:
Reliability engineering: The Birnbaum-Saunders distribution can be used to model the reliability of components or systems.
Risk analysis: The Birnbaum-Saunders distribution can be used to model the risk of rare events, such as natural disasters or financial crises.
Decision making: The Birnbaum-Saunders distribution can be used to make decisions under uncertainty, such as decisions about how to allocate resources or how to invest money.
Overall, the Birnbaum-Saunders distribution is a versatile and powerful tool for modeling data. It is easy to estimate and use, and it can be used to model a variety of data sets.
G-and-h distribution
The g-and-h distribution is a continuous probability distribution that was developed by John Tukey in 1977. It is a two-parameter distribution, with the parameters g and h. The g-and-h distribution is a generalization of the gamma distribution, and it can be used to model a variety of data sets, including data sets that are skewed or have heavy tails.
The g-and-h distribution is defined as follows:
f(x) = g h x^(g – 1) exp(-h x) / Gamma(g),
where:
- f(x) is the probability density function of the g-and-h distribution.
- x is the random variable.
- g and h are the parameters of the distribution.
- Gamma(g) is the gamma function.
The g-and-h distribution has a number of properties that make it a useful tool for modeling data. These properties include:
- The g-and-h distribution is flexible, and it can be used to model a variety of data sets.
- The g-and-h distribution is robust, and it is not sensitive to outliers.
- The g-and-h distribution is easy to estimate, and there are a number of software packages that can be used to estimate the parameters of the distribution.
The g-and-h distribution is a useful tool for a variety of applications, including:
Statistical modeling: The g-and-h distribution can be used to model a variety of data sets, including data sets that are skewed or have heavy tails.
Risk analysis: The g-and-h distribution can be used to model the risk of rare events, such as natural disasters or financial crises.
Decision making: The g-and-h distribution can be used to make decisions under uncertainty, such as decisions about how to allocate resources or how to invest money.
Overall, the g-and-h distribution is a versatile and powerful tool for modeling data. It is easy to estimate and use, and it can be used to model a variety of data sets.
