A phase type distribution or PH distribution (not to be confused with the “pH” distribution used in biology) is the distribution of absorption times or hitting times in certain kinds of Markov jump processes [1, 2]. In other words, it’s a distribution of the time to absorption into a finite state (0) in a Markov chain [3]. In their simplest form, PH distributions are convolutions and mixtures of exponential distributions.
Any phase type distribution can be deconstructed into a Markov chain (a set of states plus a transition matrix). As these distributions can be represented by Markov chains, matrix-based computer algorithms allow for their very efficient evaluation [4].
PDF / CDF for the phase type distribution
The PH distribution is intertwined with the exponential distribution because an assumption in Markov chain analysis is that waiting times have an exponential distribution.
A phase type distribution with parameters α Q and Ξ has the CDF:
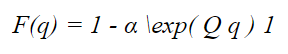
And PDF
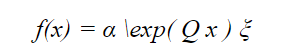
Applications of the Phase Type Distribution
Phase type distributions are used to model positive random variables, especially random times. For example, processing times, repair times, or time to failure in manufacturing systems [4]. However, their use isn’t limited for manufacturing. For example, Coxian phase-type distributions—a sub-type of Markov model for duration until an event occurs in terms of a sequence of latent phases— have been applied to healthcare settings [5]. Other uses include distances between DNA mutations and service times for agents in queueing systems.
A major downside to using a phase type distribution is the assumption of an underlying exponential distribution. Many real-life random variables do not follow an exponential distribution. For example, the Weibull distribution is often a better model for electronic component failure times[6].
References
[1] Bladt, M. (2005). Review on Phase Type Distributions and Their Use in Risk Theory. May, Astin Bulletin 35(1):145-161
[2] O’Cinneide, C. (2017). Phase-type distributions and invariant polytopes. Retrieved Aprril 8, 2021 from: https://higherlogicdownload.s3.amazonaws.com/INFORMS/50069173-2ea8-479b-baa7-2071ed7cd5dc/UploadedImages/2017-Marcel_Neuts_Lecture_.pdf
[3[ Osogami, T. (2005). Definition of a PH Distribution. Retrieved April 8, 2021 from: http://www.cs.cmu.edu/~osogami/thesis/html/node40.html
[4] Christian Commault & Stéphane Mocanu (2003) Phase-type distributions
and representations: Some results and open problems for system theory, International Journal of Control, 76:6, 566-580, DOI: 10.1080/0020717031000114986
[5] Marshall, A. & McClean, S. (2004). Using Coxian phase-type distributions to identify patient characteristics for duration of stay in hospital. Health Care Manag Sci. 2004 Nov;7(4):285-9. doi: 10.1007/s10729-004-7537-z.
[6] Komarkova, Z. (2012). Phase-Type Approximation Techniques. Retrieved April 8, 2021 from: https://is.muni.cz/th/ysfsq/thesis.pdf