What is the Lomax Distribution?
The Lomax distribution is a heavy tailed distribution originally proposed by Lomax (1987), who used it in his analysis of business failure lifetime data. The distribution, which is basically a shifted Pareto distribution, is widely used in survival analysis, and has many applications in actuarial science, economics, and business.
Parameters
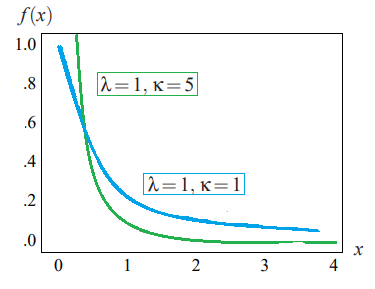
Two parameters define the distribution: scale parameter λ and shape parameter κ (sometimes denoted as α). The shorthand X ∼ Lomax(λ,κ) indicates the random variable X has a Lomax distribution with those two parameters.
The probability density function for the Lomax distribution is:
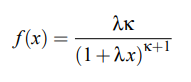
For all x, λ and κ greater than zero.
Variants
Variants of the Lomax may have more than the basic two parameters. For example, the beta exponentiated Lomax is a five-parameter continuous model (Mead 2016 ).
Many other variants of the Lomax distribution exist, including:
- Exponential Lomax
- Exponentiated Lomax
- Gamma Lomax
- McDonald Lomax
- Poisson Lomax
- Power Lomax.
- Transmuted Lomax
- Weibull Lomax
- Weighted Lomax
These are just a few: there are many more. New variants are being proposed all of the time. For example, see Oguntunde et al’s 2017 proposed new generalization.
References
A. Hassan and A. Al-Ghamdi, “Optimum step stress accelerated life testing for Lomax distribution,” Journal of Applied Sciences Research, vol. 5, pp. 2153–2164, 2009.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
K. Lomax. Business failures: another example of the analysis of failure data. J Am Stat Assoc. 1987;49:847–852
M.E. Mead. On Five-Parameter Lomax Distribution:Properties and Applications. Pakistan Journal of Statistics and Operation Research. Vol 12. No.1. 2016.
E. Oguntunde et al. “A New Generalization of the Lomax Distribution with Increasing, Decreasing, and Constant Failure Rate.” Modelling and Simulation in Engineering Volume 2017.